Month: November 2017

Persistence and Creativity

I spent six hours yesterday watching students take final exams. Three two-hour shifts. Sigh…

My last group taking an exam was my AP Calculus BC team. They had 24 multiple-choice questions and four free response questions, so they had to be efficient in their problem-solving. One of my students asked me about a multiple choice question that troubled him. It was an infinite geometric series question. This student joined our school, and our country, last year as a freshman. He place tested so highly that he started in AP Calculus AB. However, it has become apparent that there are a few facts/skills that he does not have at his command. This is rarely a problem since he is so creative. On this question, he did not have the formula in his brain for calculating the sum of an infinite geometric series. He could have listed out a handful of terms to look for convergence. He could have shrugged his shoulders and guessed since it was one of twenty-four questions. Instead, he wrote a short program on his TI-84 that gave him increasingly good approximations until he saw one of the answer choices emerge. He did this in the middle of a two-hour exam! He asked me afterwards and just laughed when I showed him how easy this problem could have been. I am convinced that he will remember this formula forever now, but I am also convinced that I will remember this story forever now. His ability to problem-solve in this situation is SO much more powerful than having a formula at his command. It is interesting that this happened on the same day that I sent our a question on twitter about the use of formula sheets on assessments. I am disinclined to use formula sheets, but I could be convinced otherwise. Here is a story that would have never happened if a formula sheet was present.

I am going to cross post this over at the One Good Thing blog space.

 

Optimistic

Another quick post. We are in exam week here at my school. I have ALL sorts of thoughts about term exams and why we do them, but those are for another place rather than this public forum. I have written about our department’s decision to move toward a test correction policy. I am so so so optimistic about our exams this week. I really believe that we will see largely improved results because the students have been more actively involved with examining their tests and reflecting on what went right and wrong on their tests. They have been talking to each other and comparing ideas. They have been talking to their teachers about how to fix their problems solving approaches. Our department exams are mostly on the next to last day of exam week. This will work against our students as energy levels start running low. Despite this, I am hopeful that we will see a different level of engagement on these cumulative exams. I will report back either way in a week or two, but I feel good based on what I have seen in the past week of reviews in class and from watching and listening to kids in the hallway as they work together.

Another Fun Problem Debate

A super quick post this morning. On my last problem set for AP Calculus BC I included the problem below:

A 10 m rope is fastened to one of the outside corners of a house, which has the form of a rectangle, 6 m long and 4 m wide. A dog is fastened to the rope. What is the perimeter of the region that the dog can access?

I have asked a form of this question a couple of times over the years. One year I did not mention that the rope was on the exterior of the house and I had a student assume that the dog was tied to a leash inside the house. I fixed that mistake.

A GeoGebra sketch below shows the image I have in my head for this problem.  

My answer to this question, and the answer that 11 of my 14 students had, was that the perimeter is 20π. Two students argued that the answer should be 20π + 20. Their argument is that the borders of the house, the sides of the rectangle in the drawing, are also part of the perimeter. I loved the debate that ensued and most students migrated to this point of view. I reflexively thought of perimeter as exterior, while these two students argued that perimeter is boundary. I think I agree with them and I LOVE the fact that they cared enough to debate this on a problem that counted for one point out of about 400 something for the term. I also LOVE that students who got their answer marked correct started arguing against the answer that they arrived at.

AP Calculus BC – A Lovely Debate

It has been WAY too long since I posted. Energy has been scattered in a number of directions lately…

 

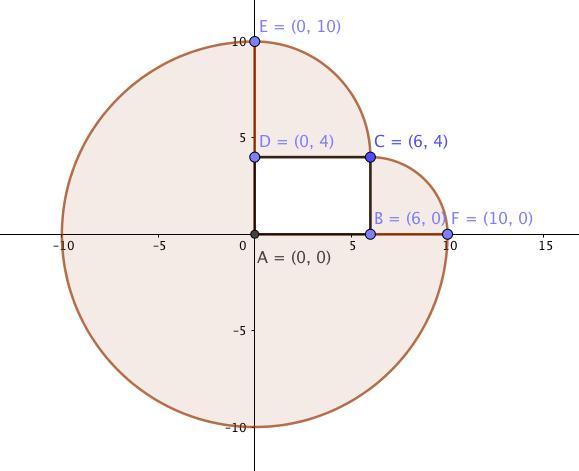
Yesterday in AP Calculus BC their sixth problem set of the year was due. I heard quite a bit of debate among my young scholars about one question in particular. Here it is:

I wish I remembered where I found this problem. I know I have used it in the past but I do not remember much debate about it. A little background about how I approach these problem sets before I relate the conversation we had. We are on a seven day class rotation in our new schedule. This rotation sometimes even includes two weekends. I assign a problem set the first day we meet on each rotation and it is due the first day of the next rotation. My students have time to wrestle with these problems, to ask each other questions, ask me questions, look up ideas/clues/data/etc. These are sets of ten problems and they only count ten points. All of the problem sets together count about as much as one test in a term. By the time the term is up, each problem set will end up weighing about 2 – 3% of a term grade. I grade them pretty easily, looking mostly for thoughtful process and I am willing to deal with half points which feels a bit silly but it honors thoughtful work rather than whacking them for some little mistake. Anyway, the point here is that these should be low stress and they should encourage collaborative thought and work. I have been clear that I encourage them to think together. Anyway, when they came into class yesterday there were a flood of questions for each other about fine points of interpretation for this problem and students were asking me about two distinct interpretations of part b of the problem. I loved the debate, I just wish it had been happening more than 2 minutes before the work was due. The primary debate was whether to answer part b by interpreting the year as the interval from 0 to 12 or whether to interpret it as 1 to 13. Our friend GeoGebra helped us a bit. Three screen shots below: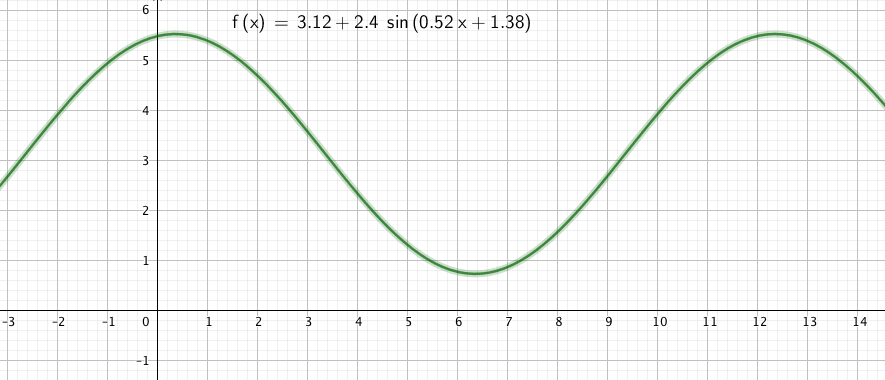 

Now, the curve with the integral from 0 to 12 highlighted: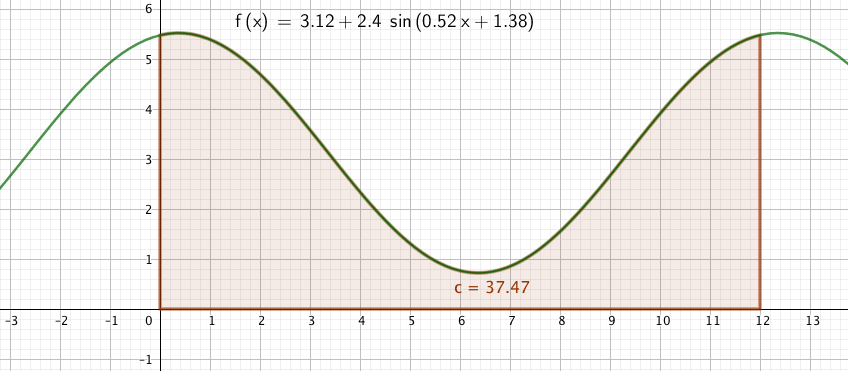 

Finally, the curve with the integral from 1 to 13 highlighted: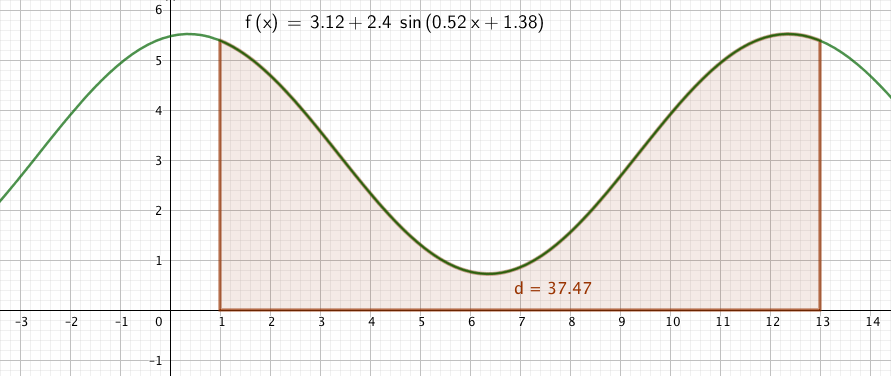 

Nice, right? The area is the same according to GeoGebra. What followed was such a highlight of my day. Intense debate about why these seem to be the same. One student notes that the obnoxious coefficient for x in the function yields a period of essentially 12. Not a surprise, right? Nice observation. A nice debate about the limits. Is 1 the end of January or the beginning? I feel it needs to be the end of the month the way the problem is written, so I came down on the side of 1 to 12 as the proper integral. An observation about the symmetry of right Riemann sums where some months have overlaps and others have underestimates. Another nice observation.  One student questions this model because he notes, as a northern city, Seattle should have more rain in the warmer weather months rather than have this mediterranean rainfall pattern. Wow. I pointed out that I know people who lived in Seattle and have visited there and that this is indicative of what I know about the area. I do not think that this would have ever occurred to me! A debate about whether we simply want to add f(1) + f(2) + f(3) + … + f(12) rather than integrate. One student mentions that he looked up the yearly rainfall in the Seattle area and the answer he found was pretty close to our integral. Good golly, that made me happy. A student questioned whether I wanted two answers to part a. I admitted that the word extreme, in this context, only made me think of a Maximum. I admitted that I should have been more careful than to make that assumption and I should include the minimum in the answer to part a as well.

We have a test today, so I pivoted the class conversation toward some practice problems but I felt that there was probably still more to discuss about this problem. Days like yesterday remind me of how spoiled I am that I get to do math with a group of scholars that are willing to engage in energetic debate about math. They are rarely interested in just knowing the answer, they seem to genuinely enjoy to process that gets them there. I am not going to pretend that all 15 students were actively engaged joining in with their ideas. I will say that there were all at least attentive and willing to let the conversation flow without pointing out, anxiously, that we need to talk about the upcoming test.

We decided a number of years ago to teach BC as a second year Calculus course at our school. We know that many of our students can accelerate through the BC curriculum in one fast year or by buying some Precalculus Honors time, but conversations like this one would be hard (not impossible) to find time for. Every year I hear a scholar say something along the lines of ‘I knew how to do this before but now I think I know why it works.’ Statements like that one, and conversations like yesterday’s make me feel good about this curriculum decision we made.