This year I am teaching Precalculus Honors at my school (in addition to two different levels of Calculus) and I have not taught this course since the 2010 – 2011 school year. Last weekend, as I was planning ahead a bit, I realized that trig angle addition identities were coming our way. I have to admit that I have been entirely unsatisfied with how I dealt with this in the past. Most texts have some sort of distance formula based derivation of the formulas and I have read through them over and over never really satisfied that I could add much to the presentation. I generally presented these as facts and tested out a handful of examples to see that the formulas verified what we already knew to be true from the unit circle. A pretty unsatisfying situation. So, I did what I do. I sent out a call to twitter for help and got the typical handful of helpful responses. One really stood out and I tried it out in three of my classes. Tim Brzezinski (@dynamic_math) sent me a link to one of his lovely GeoGebra explorations. You can find that link here I am including a screenshot below to help you understand what we were able to accomplish due to Tim’s clever design (and his endless willingness to share!!!)
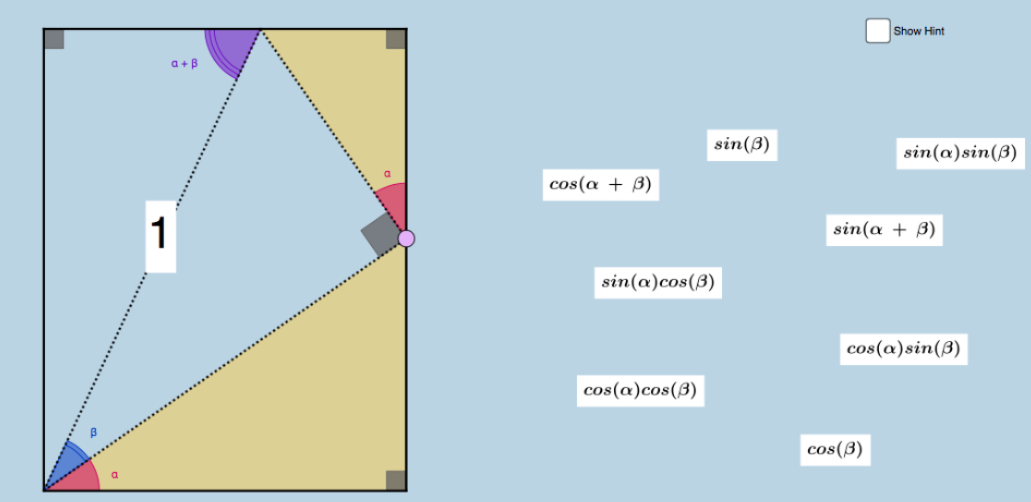
The students are presented with the above image and the very simple facts that this is a rectangle and that the two yellow triangles are similar. The point on the right side of the triangle is movable. A few things right off the bat struck me as wonderful here. We talked about WHY we could know that the yellow triangles were similar. So, we had the opportunity to remember the AA postulate. A student in one of my classes knew that the upper angle is alpha + beta because it is the alternate interior angle of the lower left corner angle. Super sweet! I was going to present a boring conversation about 90 – alpha and 90 – beta on the top. So, I liked that aspect right off. I also LOVED the aspect of how open this construction is AND the fact that it was not at all obvious to my students what we were about to discover. Pretty cool.
I ran this first for my Precalculus Honors kiddos and had each small group discuss where the wages need to go then we put our thoughts together. After a (very) gentle reminder of the structural properties of rectangles, we realized that we had discovered the angle addition formulas for cosine and for sine. An interesting response followed. One of my more curious and driven students asked ‘Don’t we have to prove this?’ I think that this speaks volumes about the natural response to the idea of ‘proof’ in our students. This exercise seemed clear and concise. Couldn’t qualify as a proof, right? Now, I am not fooling myself here. There is still a great deal of simply committing these formulas to memory at the end of the day. But I am convinced (CONVINCED!) that this feels more meaningful now. My kids were able to see and derive for themselves these relationships. They stopped and thought about similarity, about ratio definitions for the cosine and sine functions, and about the structural requirements of calling something a rectangle. I went on to tell them that they do not need to commit to memory double angle formulas because they come straight from here. Most students don’t take my advice on things like this, they feel safer simply consuming memory space with formula after formula, but that is another issue entirely.
After this went SO well with my precalc honors kiddos I unveiled it in my Calculus Honors class. We were just getting to the point where we were dealing with derivatives of trig functions and I knew that the chain rule was about to be laid on top of this. I guessed that this would be a great exercise to jog their dormant trig memories from last year. Again, in each section of Calc Honors, small group conversations led directly to sharing of ideas and a quick dissection of the diagram. I am pretty sure that these conversations woke up some sleeping facts in their brains and I hope it pays off in the form of quicker recall and comfort when we lay the chain rule on top of the standard trig derivatives soon.
Many thanks to Tim and to all the others who shared out ideas when I sent out my call for help. My students don’t really understand how much better their education in my room is due to the network of supportive, smart, creative folks out there. I do make an explicit point of telling them when I am using ideas/activities from others to help make all of this clear. The subtext I hope sinks in is this – If you have an interesting questions, send it out to the world. You’ll get some interesting feedback.