Right before the Christmas break my Calc BC class was up tot heir elbows in new integration techniques. One of the old skills that comes into play often in this unit is the idea of long division as a way to rewrite rational expressions. All of my students have known how to do this but without having exercised that skill in some time, there is a bit of grumbling about it. I presented the following problem (or one very similar to it)
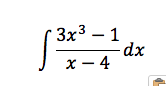
My intent was that my students recognize that they want to ‘reduce’ the fraction so that the numerator is a lower degree than the denominator. Long division makes this magic happen and then logs come into play in actually evaluating the integral. At least one of my students did not quickly recall long division. But, rather than ask me for a refresher, Allen rewrote the problem as follows:
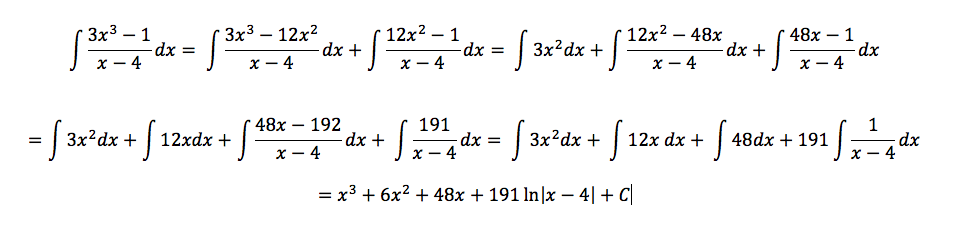
He explained his reasoning and I will paraphrase as well as I can from a conversation that happened more than two weeks ago. He recognized that the numerator had a leading term that could be expressed as a multiple of the leading term in the denominator. So he introduced a term in the numerator (and then subtracted the term he introduced) so that he had a leading piece of the integral that is a simple polynomial. The 12x^2 term now served as a multiple (again!) of the leading term in the denominator. Simply adding and then subtracting 48 x allowed him to simplify the next piece of the integral. One more iteration (subtracting and then adding 191 this time) got him to exactly where he would have been if he remembered long division.
I have to admit that I would love it if he remembered long division, I think it is a useful skill and probably saved him a little time. However, after listening to him explain his reasoning I realize that he displayed a pretty deep level of understanding here about how this expression can be rewritten in steps. The level of analysis and understanding here (I think) far exceeds simply remembering an algorithm learned in precalculus days. This has me debating how I want to approach the instruction of long division of polynomials moving forward. I’d love to hear your thoughts on this here in the comments or over on the twitters where I am @mrdardy