Late in December my school replaced my 10 year old iPad with a new model. I’m kind of spoiled, my school supplies me with a laptop that gets upgraded every four or five years and they have also supplied me with an iPad. The combination of getting this new iPad along with transitioning away from virtual learners allowed me (encouraged me!?!) to do some pretty quick learning. Since August 2020, I have been tethered to my laptop and a graphics tablet. Everything I write in class has been on an online paper source called BitPaper and I left records of all of our class discussions and work there and posted the links to our Google Classroom. The two drawbacks were (1) I could not move and rove around class at all and (2) the BitPaper does not act like Google docs. If I look at it and another person is already there, any change they make such as scrolling through the notes also effects my screen. It kind of made my students crazy. So, during break I ordered an Apple Pencil and, at the urging of some of my students, started learning how to use an app called Good Notes. Late in January I finally felt comfortable enough and I left my MacBook and Wacom graphics tablet and started projecting our class from my iPad using Good Notes. I can convert every class days’ notes into a PDF and upload them to a shared folder so my student own their own copy of the class work every day. I am getting comfortable (or, at least, MORE comfortable) grabbing screenshots and cropping them and pasting them. I can add blank pages between things when class work takes more space than I anticipated, it is more natural to write directly on my iPad than it was to write on a graphics tablet, I can move around the classroom again, and the iPad is just more mobile even around my house. I am more likely to jot down some quick ideas/notes in preparation for a class. Most importantly, my students are watching me learn and grow proficient at a new skill in front of them. Most of my progress is in the form of me asking a question out loud and having some student(s) give me a tip. Visible learning is a good thing to model. Learning from my students is a GREAT thing to model. Seeing a teacher excited about learning something new makes it at least a little more likely that my students might be willing to get excited about learning a new skill. The past couple of weeks have been rejuvenating as I work toward mastering (yet another) new way of having my classroom operate.
Category: Classroom Practices
Well, It’s been a while
I am out of practice at writing here, let’s see how this goes.
My last post was 14 months ago for all sorts of reasons, most of which have to do with the fallout of the pandemic. The spring of 2020 was sheer chaos as we were all trying to figure out how to teach virtually. The 2020 – 2021 academic year saw a multitude of rules restricting how we could interact with each other when we were in person (which, for our school, was the great majority of the year) and a couple of retreats into virtual schooling. I had students in front of me and students on my computer screen all year long (at least when we could have people in the same room!) and I know I was not alone in learning how to deal with that. I had all my students seated in rows and columns for the first time in 15 years and I had to try to relearn how to look out at a class like that. We could not sit in groups and share ideas with our neighbors at our elbows. I could not roam around the room and look over people’s shoulders and quietly share ideas and questions. None of this is news to anyone who is reading this. What I am trying to figure out is what tools/habits I’ve developed in the past fifteen months are worth carrying forward into the 2021 – 2022 academic year and beyond. There is a cliche about not wasting a crisis and I had some pretty meaningful conversations with my students about the ‘new normal’ this year. I laid out some practices that I had adopted, practices that were not part of my repertoire before COVID days. I asked them what was worth keeping and what they would be happy to never deal with again. The three features of life this year that got the biggest endorsements were (1) Scanning and submitting written work so that they could access their work and my comments at a later time. (2) My inclusion of DeltaMath into our life. (3) My use of BitPaper for classroom notes.
I want to think out loud about each of these three features.
1 – Obviously, any paper submitted and returned with notes/corrections/remarks is retrievable, even in COVID times. However, my students were really honest about their lack of organizational skills. Most papers that ever got returned got shoved into backpacks, ended up at the bottom of a locker, on the floor of their car or their bedroom, and were not accessible when it came time to study or reflect. I did not enjoy writing on their work through the google classroom and within the Kami environment. But if even a small portion of my students actually went back to the Google classroom page later to reflect, then it might (might!) be worth that time and effort.
2 – I was way too late to the DeltaMath game. I think Zach’s work there is tremendous and I got so much positive feedback from kids about the guided practice and videos available to them there (I paid for a plus membership so my students have limitless (I think it is essentially limitless) access to carefully presented videos to help them work out mechanical issues and to be reminded of why math life was unfolding the way that it was.
3 – I don’t know how many people know this tool. Here is an example of one of my BitPaper note pages https://bitpaper.io/go/Bell%206%20Calc%20Hon%20Week%20of%20May%2010/HJpuKAieh
I set up a new page for each section each week so that the pages would not get TOO cluttered. I did not write on a whiteboard at the front of the room at all this year. I did all of my writing on BitPaper and students had access to these pages at any time. There are some tweaks I wish they would make. I wish there was a scroll bar to move up and down the page. I wish multiple kids could view at the same time without interrupting each other. The second wish might be a lack of understanding on my part. But that is not what I want to write about. I want to talk about what I see as a huge advantage. My students can listen in on my conversation and what their classmates are saying. They can jot down quick notes or reminders to themselves, but they do not have to feel any pressure at all about transcribing while listening. They can look at class notes later and listen and think more efficiently in real time. I had a discussion about this tool and about the fact that I intend to use it again next year (or a different tool that might be better if someone can steer me to one!) and the response I got was that note taking is a vital skill and they need to work on this. I tried not to react negatively but inside I was sure feeling some serious skepticism about this claim. It feels obvious to me that listening and thinking and talking are more important than being a stenographer. If I am wrong here, if I am missing something important, I hope to hear it either in the comments or over on twitter where I am @mrdardy
There were SO many new tricks/tools that I tried this year but these three were the ones that resonated with my students. I would love to hear some reaction to these ideas and also hear about successful new tools/ways of thinking that infected your classroom during the pandemic.
Empowered Problem Solving / Empowered Teachers
Not too long ago according to my calendar, but a long time ago now according to how the pace of school life moves, I finished an online workshop run by Robert Kaplinsky. The workshop, in six modules, was called Empowered Problem Solving. The modules were released on a weekly basis and were centered on videos of a workshop that Robert ran. These videos were accompanied by some outside reading in the form of blogposts and some PDFs. There were question prompts to encourage lively conversations on a message board, and there was quick support through emails from Robert and others working with him in the one or two cases early in the course when questions popped up about navigating the interface that they had set up. I did not recognize the names of folks on the message board there but I came to develop a sense of kinship through our conversations over the course of almost two months. Several themes emerged, of course, and it was interesting to go back through message boards from earlier lessons to see how my thinking was moving/growing and how the conversations deepened over that time. Looking back now, a few weeks after the course ‘ended’ [we still have access online for at least another month to revisit ideas and to help deepen our understanding/comfort with the ideas of the course] at a folder I created with documents that Robert organized for us, I realize that it will probably be out extended Christmas break when I can really digest and inject some of the habits of mind that are encouraged in the course. It made me think of my journey in grappling with/enacting/understanding the principles of inquiry and open-ended problem based lessons in the math classroom. I was forutunate to have had a Master’s Degree class in 1987 (before my teaching career began) called Mathematical Problem Solving. My grad school advisor, Prof Mary Grace Kantowski earned her Ph.D. in 1974 and her dissertation was Processes Involved in Mathematical Problem Solving, so I got a dose of this working with her and taking her class. I entered the high school classroom in the fall of 1987 and I have been honing, adapting, striving, to really figure out how to incorporate something more meaningful than practice exercises with my students. I was further energized by my first visit to the Anja Greer Conference at Phillips Exeter (I know it was between 2001 and 2005 but I cannot remember for sure what year it was) when I met Carmel Schettino and learned from her about problem solving in the math classroom and I am certain that this was my first exposure to the Exeter problem sets . The conference was mind-blowing and I was fortunate enough to attend one other time since then. Carmel’s work and advice energized me further and I started writing my own modest problem sets. Later, I wrote my own Geometry text that our school used for five years and in the process of that, I wrote HW for the course in the form of smaller problem sets. I have been fortunate enough to attend a summer think tank styled workshop that Carmel ran. I went with three colleagues to a workshop run by some folks from Packer Collegiate Institute in Brooklyn last year. I visited the Peddie School in New Jersey with three colleagues and we saw what they had done with their curriculum. Our school was visited by a member of the math department from Saint Andrew’s School in Delaware and he shared what they have done with their curriculum. All of these experiences led me to want to enroll in Robert’s online classroom and it was well worth my time and energy and the school’s investment of professional development funding. Conversations are happening in our school about the direction we want to go for our students and the visits and workshops last year helped prompt these conversations. The ideas and resources from Robert Kaplinsky’s workshop will be immensely helpful in moving this conversations forward.
All of this is a long winded way of me saying thank you to Robert, to Carmel, to the folks at Peddie who welcomed us, to Eric Finch from St. Andrew’s in Delaware, to my advisor Prof Kantowski. All of these voices throughout my career seem to be pointing the way to a more meaningful way of teaching and learning mathematics. Robert will be running his workshop again in February and March and I encourage you to take part. Whether you are just beginning to grapple with the ideas of running your classroom as a place of open inquiry and driven by problems (rather than exercises – a distinction that Prof Kantowski often discussed) or if you have been working with these ideas for years and are looking to be re-energized or more organized, this will be a great experience for you.
Thinking About Stories
One of the newer initiatives at our school is to help students listen and tell stories. We partnered with an organization called Narrative 4 (you can see their work here) I am simplifying the mission here a bit but the idea of storytelling is on my mind for a number of reasons. Next Wednesday our sophomore and freshmen students will participate in a Narrative 4 workshop sharing songs that mean something to them and explaining why. I love the power of stories and am prone to share them myself to try to make a point. I was reminded of this in the Empowered Problem Solving (#epsworkshop) run by Robert Kaplinsky. He made reference in one of the videos in a study module to ‘the story we are telling in our math class’ and this made me think of a recent frustration with our precalculus book. It all comes together, at least in my mind! Anyway, we are starting our unit on conics and our text, as many do, suddenly changes format of how a parabola equation is presented. Our students are used to y – k = a(x – h)^2 and this format makes sense to them. We can easily adapt this to x – h = a(y – k)^2. Suddenly, we are talking about the directed distance from the vertex to the focus and we introduce this new constant p. Okay so far, right? But suddenly, my students see 4p(y – k) = (x – h)^2 and they see 4p(x – h) = (y – k)^2. Why? It is pretty simple to let them know that the a that they have grown to interpret has a side personality as 1/(4p) It is easy to find a point on the curve and show distances that are equal to each other. I do not want to ignore the examples in the text because my students use it as a reference and a resource. I also do not want to stray from a meaningful way to write equations simply because of the whims of our textbook author. I also suspect that so much of what kids learn in school feels like an arbitrary set of equations and definitions and I want to battle that. I want the story in our math class to be that this is a journey together that builds on what we’ve known before. A journey that ties ideas together. A journey that feels logically coherent and consistent to the best degree that I can possibly make it. Lofty goals, I know. I just find the weird changes like the one above undercut that sense of logic, consistency, and damage the connective tissue of ideas that I try to nurture. I am almost certainly overreacting to this weird quirk of Precalc texts, but that feeling was amplified when I thought about our storytelling exercise at school and tried to reflect on Robert Kaplinsky’s message in our workshop. I love it (LOVE IT) when my brain is agitated by these ideas, when I see connections and themes in my life. I try to share that joy (agitation sometimes!) with my friends, colleagues, students, and you, my dear readers.
Another New Beginning – Around the Corner
On Monday I report for beginning of the year meetings for the 33rd time. As usual, I have thoughts scattered all about and, as usual, I am going to try to use this space to help whip those thoughts into shape.
This morning I read the latest NCTM email and there was an essay included written by President Berry. In his essay, he challenges us to think about our why. Why do I teach math? He suggests that figuring out the why is a HUGE step to making our classrooms more coherent and productive. In the essay he links to a couple of posts and my favorite of them is from David Wees. You can find it here and it is well worth your time.
David’s post made me think about a time when I was struggling a bit with thoughts like these (I have a post about that here ) and I was thinking that the beginning of a new year might be an excellent time to be explicit with my students about the teacher that I try to be and to try and tease out from them the teacher that they feel that they need. I think back to a story about a former student. He was a brilliant student and has gone on to do some serious financial analyst work in his life. He uses math skills and habits of mind regularly in life. When I taught in New Jersey Chris (the former student in question) lived in Manhattan and he and I would periodically meet for lunch. He told me a story one day. He was working in a small office at the time and had been struggling with a challenging case. My memory is that he said he had been working off and on with a certain problem for a few days. He told his boss that he was going to take a long lunch to get away from this problem and clear his head. Chris told me that when he returned he found some post it notes on his file folder with some questions/suggestions from his boss. Chris said ‘Jim, he reminds me of you. He asks questions I would not have though of asking.’ I have considered this to be the best compliment I think I have received as a teacher. This brilliant person – WAY smarter than me – one who I taught for four math classes (he and I started at a very small school) doesn’t remember a certain lesson. He didn’t point to some trip that we went on together (he was an expert Brain Bowl member and math team member, both activities I supervised) No, he remembered that I asked him questions he would not have thought of on his own. I was prompted to think of this yesterday when an old post by Christopher Danielson was referenced on twitter. You can find that post here. Also, well worth your time as is David’s post above.
So, I guess my question here (see what I did there?!?!?) is this – Is it meaningful to my students to have me share some version of the story above so as to clue them in to my priorities? Is it meaningful to share my priorities in a personal way as an avenue to have them think about theirs? After all, the classroom is theirs more than mine. I need to find a way to recognize and respect their needs in a way that supports what I believe (what I think I know) about teaching and learning. I want to be explicit in discussing our goals and it feels that a personal story about what motivates me to do what I do might be a smart way to do this.
Thoughts? As always, please share any wisdom here in the comments or hit me up over on the twitters where I am @mrdardy
The Case For, and Against, Test Retakes
I am overdue in writing about a high energy twitter exchange I was engaged in recently. I am going to include a few links here in this post that will help give some background to the conversation.
First, many thanks to those on twitter who are willing to engage and get my brain moving. In this particular story the star twitter pal is Kristie Donavan (@KristieDonavan) who went on quite a twitter tear and wrote a GREAT blog post. First, I will link the article that started the whole discussion.
A colleague shared an article from Edutopia with me. You can find the article here The article is called The Case for not Allowing Test Retakes. Now, the idea of test retakes/corrections is something that has been on my mind for awhile. Two years ago, after a wonderful PD session with Henri Picciotto (@hpicciotto or over at https://www.mathed.page ) our department adopted a policy of test corrections. You can read my original blog post about it here. Well, last year the department voted to move away from that policy based on a number of concerns that they had about how kids dealt with the policy. Many of their points were raised in the Edutopia article linked above. We have some new admins at our school in the last couple of years and there is reason to believe that we will be urged to move back to some form of test corrections or retakes. That is why my colleague sent me the link in the first place. I tweeted out a link to the article asking for insights and boy did I get some. Most vigorously from Kristie. Who sent a tweetstorm and wrote an awesome post. Here is where you can find Kristie’s post, I urge you to read it. So, what I am wrestling with is a real sense of hypocrisy that might be simply the result of a strong but unsound argument presented in the Edutopia article and in other debates/discussions about educational goals, student motivations, balancing workload, etc. When Henri was with us one of the things he said that REALLY resonated with me was this – ‘When you are grading you help one student. When you plan for a class effectively you help all of your students.’ [I admit I might be mixing his words a little, but the message here was clear, spend time and energy planning for your class do not get buried in grading] What he also urged, and I saw it in our policy, was to concentrate on learning not on grades. When we did our test corrections I saw kids dig into their work, they debated with each other why something was wrong and how to fix it. They engaged with their tests when they were returned instead of simply filing them away in their backpack or locker. I truly believe that my students, my youngest ones especially, benefited for the motivation to reflect that the policy provided. In the wake of an overwhelming feeling by my department colleagues that we needed to move on from that policy, I adopted a variation for two of my classes – the two where I was the only teacher. What I did was I wrote a reassessment for every test mirroring skills as closely as I could for each problem. Students were allowed to reassess on up to three of the problems that they originally took and I would average scores from the original and the retake. I wanted to minimize time and effort on their part so that they were not mired in looking backwards while we were still on the move. I also wanted to make it more realistic that we could find time during our day to make this happen. There are all sorts of tweaks I wish I had thought of, but it felt like a good faith way to try and hold on to the benefits of reflection while providing some motivation to do so. However, the time and energy spent on some much rewriting and regrading was exhausting. I found myself getting resentful and not enough of the kids were showing the same kind of benefits I expected. I also am actively struggling with what SBG would look like in my classroom. I admit some ignorance here, but my understanding from some reading and from a workshop I attended about four years ago makes me worry that my assessment strategy would not mesh well. I cannot regularly look at a problem on a test or quiz and put it in a nice box. I tend to write problems that pull different ideas together or put an old skill in a new context. Twitter pal Julie Reuhlbach (@jreulhbach) very kindly shared a folder of assessments that she uses in her SBG approach and I am beginning to dive in and try to figure out how I can make some form of this fit my life. She also hosted on her blog site a nice post about SBG. That post is here
So, here I am with about two weeks left before the beginning of my school year. I am trying to balance what would make sense for me as a teacher in my classroom with what would work for my department and what would work in our school context as we try to figure out the path that our new leadership wants to explore. All of this needs to be framed with our students in mind, they are the point of why we are doing any of what we are doing. I have an additional ingredient in my head that becomes more and more pronounced and that is the fact that my older child is now in our high school. Factors that I had been thinking about in terms of educational philosophy are suddenly feeling more urgent and more personal.
Where do I stand this morning? I worry that many of my students are SO driven by grades and by trying to balance their commitments that they are motivated to reflect and learn more by grades than by almost anything else. They tell me this year after year by saying things like ‘I would do more homework practice if you graded homework regularly’ They say this even after acknowledging that they would learn more and do better if they practiced more regularly. Given this fact (at least I am pretty convinced it is a fact) I want to have a set of classroom practices and policies in place that take advantage of this motivation and reinforces habits in a way that leads to better learning, less stress and, hopefully, better grades so that my students feel a tangible sense of their efforts. I want policies and practices that do not increase stress and put time pressures on me and my students. I want students to feel that there is equity across their classes, not to feel like they lucked into (or were cursed by) certain teachers. I think that some sense of uniformity of expectations is kind of important. I want a coherent set of principles to be visible to my students and their parents, a way to express what I believe is important about our work together.
This month I start my 33rd year of classroom teaching. At one point in my life I thought I would have figured all of this out already. I suppose the job would be less rich and rewarding if that were true.
A Fun Rabbit Hole
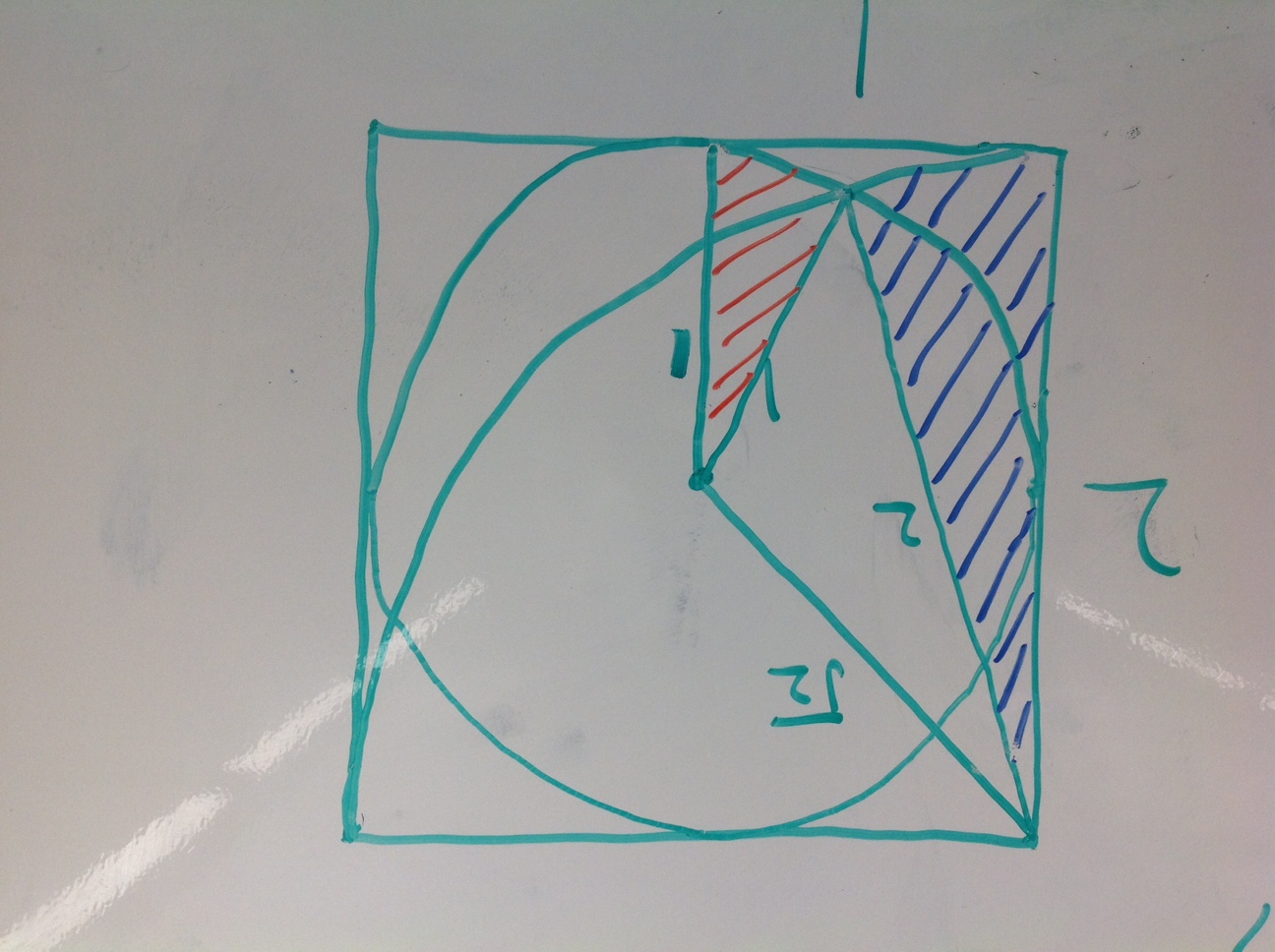
Last week – I know, it’s taken too long to write about this – my Precalculus Honors class started the day with a brief quiz. One of my PCH students named Max finished the quiz early and started sketching on his scrap paper. He showed me a diagram like this:
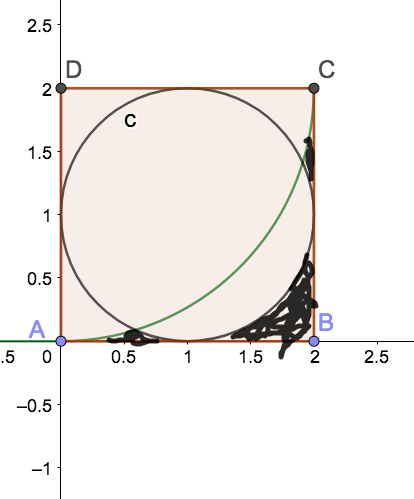
He described the problem this way – I have a square and a quarter circle coming across it. I also have a circle inscribed in the square. What is the area of these little regions? (I clumsily sketched in those regions on GeoGebra)
Well, it turns out the the topic of the day in AP Calculus BC that day was to be trigonometric substitution for integrals and this problem would be a lovely introduction to the need for this skill. AP BC was meeting for the 90 minute block and I decided that I would introduce Max’s problem, spend about ten minutes dissecting what we could and then hit a bit of a wall where I would introduce this new skill. I was pretty proud of myself and feeling very fortunate that Max thought of this question. Well, as we all know, life doesn’t always work out the way we want it to in school. I presented this problem and told them that it came up in Precalculus Honors. My BC kiddos started dissecting it right away. They concentrated on the lower left corner, they decided we should agree to a side length for the square and off they went. We decided the square should have a side length of 2 so the inscribed circle would have a radius of 1. Avoiding fractions until we HAVE to deal with them is a good plan in general, right? So, the lower region is 1/4 of the difference between the inscribed circle’s area of pi and the square’s area of 4. Good start. Next we convinced ourselves that the two remaining squiggly areas are congruent. It would have been nice if we could drop a line from the point of intersection to divide that region in two but it’s not symmetric. The different radii of the circles intersecting prevents that from being true. So, here is where I figured I would introduce this new technique. I mentioned this idea but the feeling in the room was that we should be able to answer this question using tools that a precalc student should be able to use. I was sitting in the back of the room at this point with my laptop on and a GeoGebra sketch projected on the front wall. Ideas and questions started flowing and students asked for a Desmos sketch like the one below:
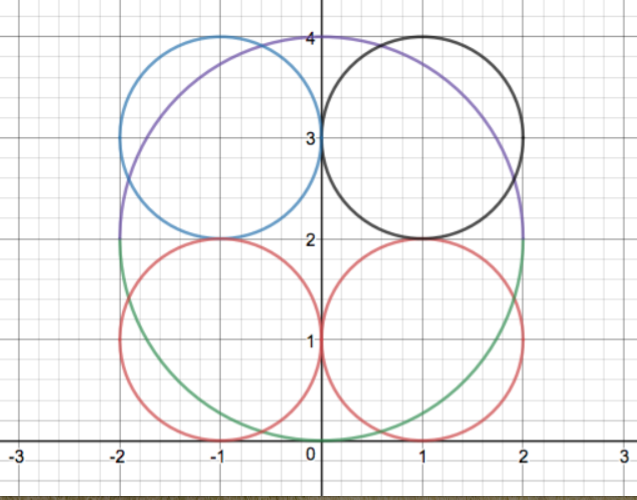
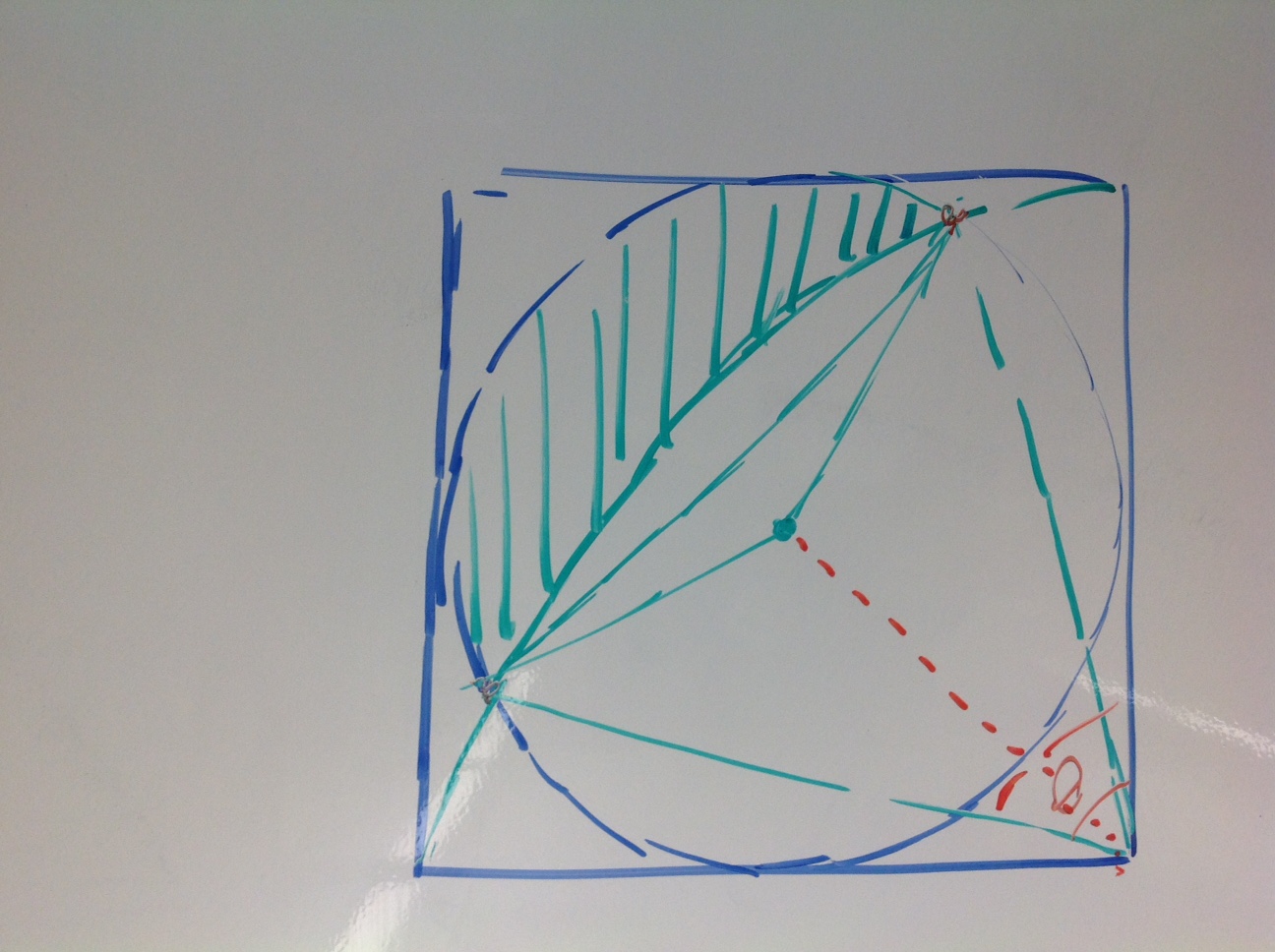
Jake proposed this and felt that the added symmetries would be helpful in discussing this problem. I asked if anyone wanted to see a point of intersection identified and we did at first but then erased that point from the conversation. We are about 20 minutes into our 90 minute class now and probably at least 5 minutes behind where I wanted to be but the energy in the room was pretty incredible. Students started going up to different boards and sketching ideas. They asked for paper printouts of the demos sketch and started moving from small table group to table group. People were debating and correcting each other and I just sat there. I was listening, I was tossing out questions, but mostly I was just watching this all unfold. The students were dusting off old trig ideas and old geometry ideas. They were debating the need/desire to have the decimal guess of the point of intersection. One student, Nick, was determined to think about this in terms of proportions and he drew a lovely argument that the area would end up being around 10% of the whole square. His classmates were unconvinced and he argued his point two or three different ways. One student, Colin, broke the region into circular arcs and argued about finding the area of a central angle. He had a great drawing but I did not capture it on my iPad. This conversation kept rambling on over the course of our allotted 90 minutes together. I proposed a couple of times that I could give them a new calculus tool but they kept waiving me off. Noon rolled around and I told them they could go to lunch. Many of them did, kind of exhausted by all of this at that point. One group of three – Nancy, Andy, and Michael – were fired up at this point and were sure that Colin had made some small mistake in his sketch. They produced this –
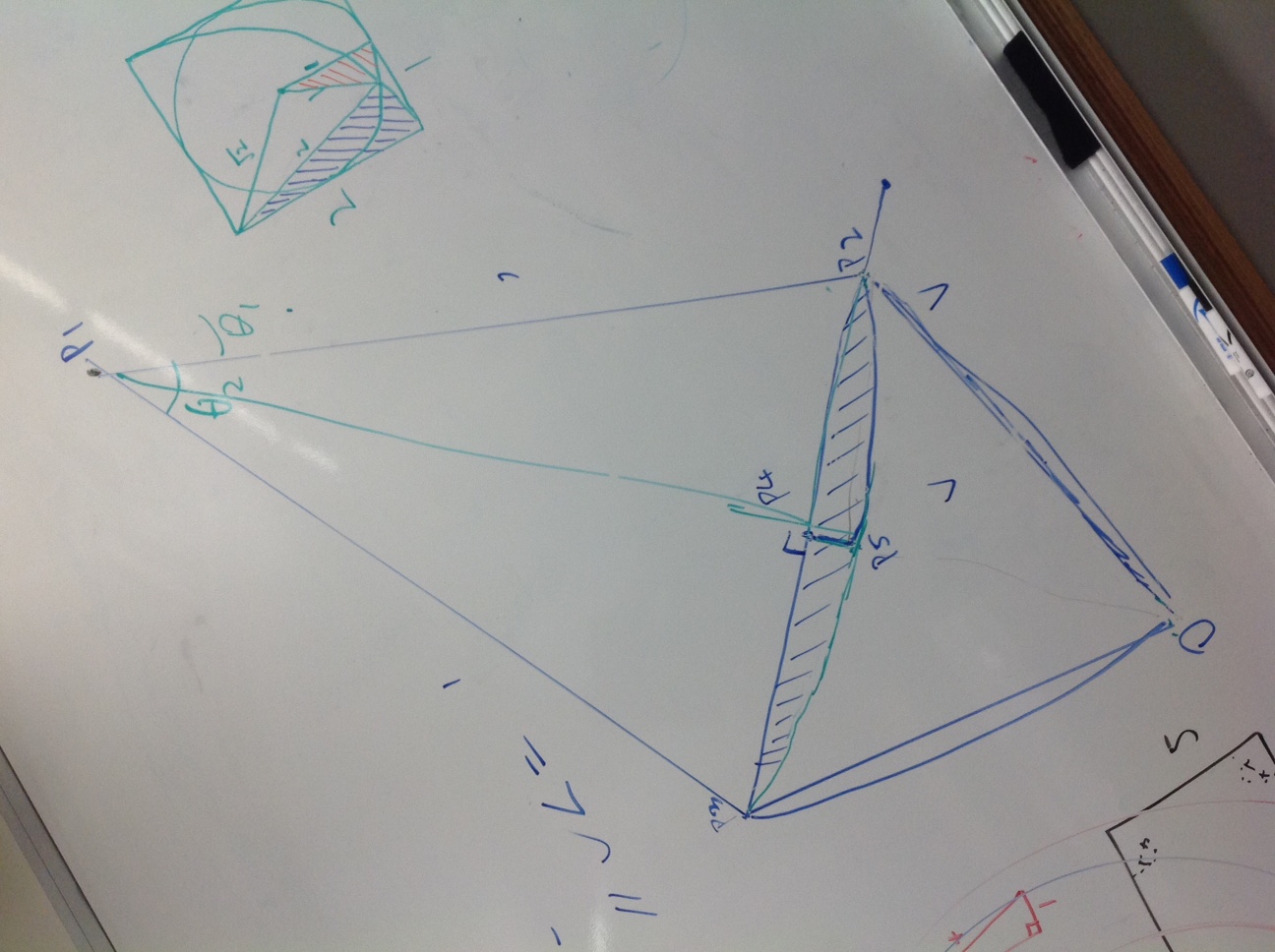
So, this sketch is pretty impressive in its detail but, more importantly, this sketch happened about 20 minutes after lunch began and after I excused myself to run an errand during lunch. During the 90 minute class, my colleague David from across the hall wandered in a couple of times asking kids to explain what they were doing. He told me that Nancy, Andy, and Michael worked for at least a half an hour of they hour long lunch debating this problem. The other thing that happened while I was gone was that Andy, Kelly, and Michael had modified my Desmos sketch on my laptop pursuing their idea. Their modification is here –
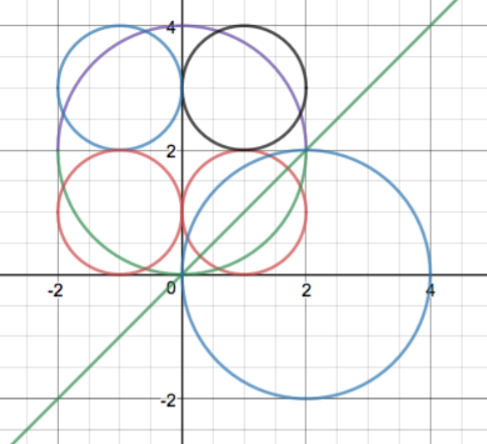
I was feeling pretty great about their perseverance, their engagement, and the amount of geometry and trig that was being remembered in the service of this curious problem proposed by one of my students. I was also more than happy to amend this week’s Calc test by taking off the one problem that relied on the trig substitution technique. I had one more class after lunch (one of my Honors Calculus sections) so I sadly erased some of the work on the board and I described the problem to that group. Some of them had already heard about it during lunch! My BC kiddos were still talking about it even after they left. At the end of the day one of our Differential Equations students wandered into my room. He said ‘I heard there was a good problem today.’ He, Owen, then proceeded to discuss the problem with Andy and Nancy who had come back to the room to discuss this. Owen dove in to the problem debating with Andy and Kelly and he produced these sketches – (the first one got rotated in translation)
I tweeted the problem out, like I do, and a former student jumped in and offered this sketch –
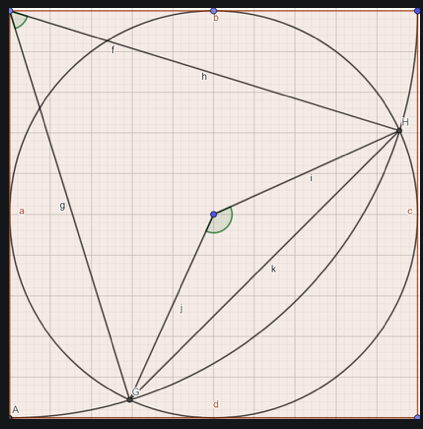
Another colleague, Adam, came by when he overheard this conversation and he attacked the problem using Google sketch up to find the ratio that Nick wanted – it was smaller than his proposed 10% neighborhood.
There is no real ending to this story, the weekend came, life moved on. On Monday my BC class was more focused on asking questions about this week’s test. My Precalc Honors kids were impressed by my enthusiasm in talking about all of this but they did not share Max’s curiosity about the question. I went home feeling pretty great about the sense of play and sense of curiosity of many of my students and my colleagues. While I cannot let everyday roll this way, I need (NEED!) to make sure to create spaces where this kind of magic can happen. I think almost all of the credit for this adventure lies with my students who are interested, motivated, curious, and persistent. I hope that I have helped them along by modeling curiosity and by being willing to let this kind of free range play happen in class.
Thinking About Trig
In the fall I will be teaching a section of Precalculus Honors at my school. I have not taught that course in about six years so I have not spent a bunch of time thinking about teaching trig functions for awhile. Our Precalc Honors class starts off with a study of Trig and I am thinking about an opening day activity that might plant a number of seeds that we will need to germinate over time. I want to play with some data that is periodic in nature and try to generate some hopefully interesting questions. Thinking along the lines of Dan Meyer’s challenge of finding an aspirin. I tweeted a bit about this and have been engaged in a terrific conversation with Bonnie Basu (@GotMathHelp) about a similar activity that I used as a demo lesson for a job interview years ago. The context is different since those students had already been a bit immersed in their study of trig but they had not been graphing yet. My goals with that group were to uncover the periodic nature of the hours of daylight, to talk about why other functions that seemed appropriate to the picture (especially quadratics) were not appropriate, to build up some sense of important vocabulary for trig graph analysis, and to simply plant some important ideas that would be explored in greater depth after I was gone. Looking back on the activity I see all sorts of tweaks I want to make and Bonnie has been super helpful in asking questions/making suggestions. Anyone who wants to take the time to share ideas or questions would certainly help make the beginning of my precalculus class this fall more meaningful and successful. I thank you in advance for any tips.
After another round of conversation on twitter that included tips from a student who just graduated from our school, I have been playing with three different data sets. I want to play with average daily temperature, high tide level, and with daylight hours. The data for the first two came from wunderground and the third data set came from dateandtime. Below are pictures of the data and Desmos links to the tables.
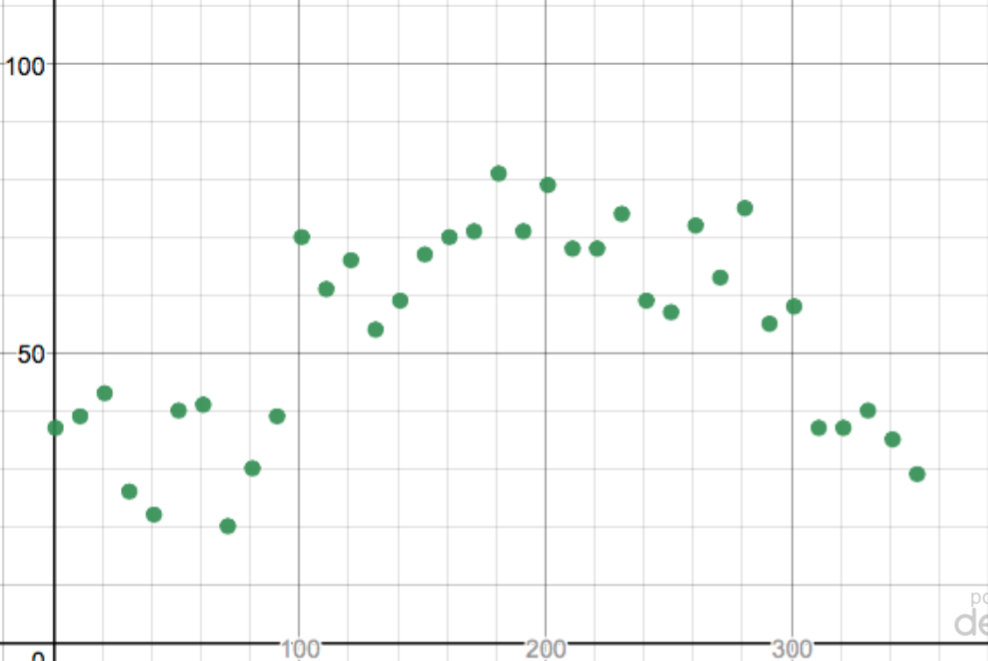
This picture (above) shows the average daily temperature in my town during 2017 at 10 day increments. You can see the Desmos table here. There are some things I like about this picture. I like the fact that the general shape can be inferred. We can talk about why it fluctuates on a number of different levels. However, I don’t think that this is a great data set for beginning to develop an idea of periodic functions. It feels too noisy to me.
Here is the picture for high tides.
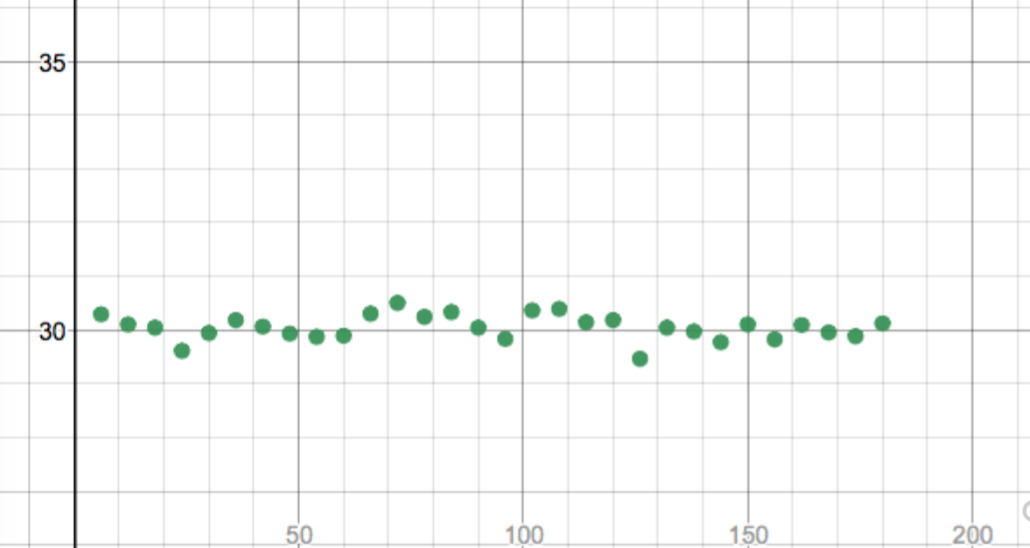
This table was built on data at 6 day intervals from the beginning of the year through June/July. You can see the Desmos link here. I would definitely ask the students to play with window sizing and I think that some powerful ideas about amplitude and vertical shift can quickly come out of such a conversation. I picked 6 day increments thinking that I would be slightly off phase with what I thought would be a period related to the full moon. A quick survey on google just talks about a 12 hour plus period so I may have been making this up in my mind. This picture feels more friendly with just a little noise involved. I might use this one early – maybe even on day one. The next one is much cleaner looking. Here is the data on length of daylight hours during 2017.
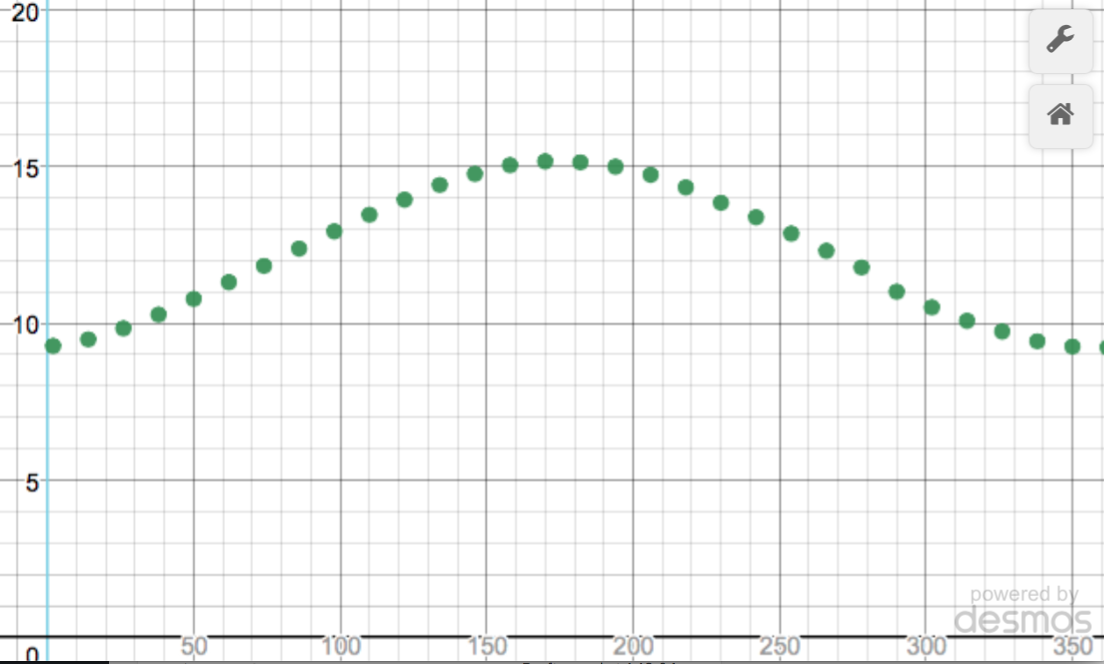
This is where my mind was when I created the demo lesson. However, this data is for our hometown here. You can see the Desmos link here. My thoughts about this data set go down two different paths. One thought is that this is clean and clear and easily explainable. One tweak I might make based on my conversation with Bonnie is that I might extend past one full year (say about 400 days or so) to make the periodicity visible not only intuitively meaningful. My second thought is that this might be too clean that it might lead my students into expecting such clean, clear periodicity in a messy world. I am probably overthinking this on the second train of thought.
I expect to have five table groups of students (groups of three in my classroom after long debating it, I accepted the wisdom shared by a number of MTBoS folks – especially Alex Overwijk (@AlexOverwijk) and my classes were better this year because of that change!) and I am thinking that each table group should have different data. I am playing with the idea of mixing up sunlight or tidal subsets of data versus simply subdividing one larger set. For example, if I go with the cleaner daylight data I can extend it to about 450 days or so and give different table groups subsets of about 35 data points each. I feel that they would benefit from seeing how the data ‘fits together’ and that individual table group decisions about amplitude, vertical shift, and period all match each other pretty well.
I would love some feedback/suggestions/questions and I thank Bonnie again for her valuable thoughts. You can drop comments here or over on twitter where I am @mrdardy
What Math Teacher Do My Students Want?
At TMC16 one of the impressive experiences was listening to the keynote speech by Tracy Zager (you can find it here ) and I remember briefly mentioning it in a post soon after the conference. Sadly, I never went back and really dissected my positive feelings about it, but I do know that one of the habits I developed after her speech was to communicate pretty regularly with our elementary school teachers more regularly when I ran across interesting math tidbits. I also know that Tracy has written a well regarded book called Becoming the Math Teacher You Wish You’d Had. I have not read this book (yet!) but the title of the book has been haunting me. I am not speaking with any deep knowledge about the strategies that she is advocating and I may be doing her a disservice, for which I apologize in advance. But as I am sitting here at the beginning of my spring break, I am thinking about what has gone right and what has gone wrong so far, 2/3 of the way through my 2018 – 2019 academic year. I also think about the phrase from Dan Meyer’s TED talk, ‘Be Less Helpful’ and this morning I want to try and wrestle with each of these phrases that are resonating in my head.
I will admit up front that my interpretations of these two phrases are my interpretations. I also need to fill in a little background to explain how I understand Prof. Zager’s phrase. I had two high school teachers who were enormous influences on me. I had the same English teacher, Mrs. Myra Schwerdt, for my junior and senior year. The way her typical class went was this – we came into class, she tossed out a question prompted by our reading assignment from the night before and then she moderated the discussion. Tossing out another question if the conversation ran dry or probing someone on an opinion/interpretation that they made. She was sort of first among equals in these conversations. I never felt that she forced us to interpret anything in any way but I also felt that we better have some backing for what we had to say. In my senior year I took AP Calculus BC from Mr. Barry Felps. A typical day in that class started off with a quick look at a new idea with Mr. Felps offering an example or two of ‘how to’ after explaining some new idea. He would sometimes go over a HW question or two from the recent past (often after his go to joke, we’d ask ‘Mr. Felps, can you do problem #12?’ He’d look at the book and nod while saying ‘Yep’. Still cracks me up a bit thinking about this…) After this, typically 15 – 20 minutes total, he’d say ‘Okay, you have work to do and so do I’ He would sit and we would work with our neighbors and friends. If we got stuck, we’d go ask him but most of the time we felt that we wanted to figure it out ourselves. We also had a study group that would periodically meet on Sundays for a combination of football, pizza, calculus, and physics. So, here I have in my mind what ‘Be Less Helpful’ looks like (to my 17 year old self for sure) and an image of the math teacher I wish I’d had (which, I feel enormously fortunate to say is a math teacher I did have)
Fast forward from 1981 – 1982 academic year to the 2018 – 2019 academic year. This year I am teaching four different classes with pretty different groups of students. I teach Geometry with the text I wrote four years ago to mostly 9th and 10th graders, I teach a Discrete Math elective to mostly seniors, I teach a non-AP Calculus class to a mix of juniors and seniors, and I teach AP Calculus BC to a mix of juniors and seniors (with one brilliant sophomore in the mix) These classes all have different needs and different inherent investments from the students involved.
It is, of course, unfair to generalize too broadly, but I think it is fair to say that the general needs/wants of these classes differ. I try to account for that, but I know that there are some tendencies in my teaching that appear in all four subjects. I ask more than I tell. I redirect questions to other students to get their input. I have student in groups of three facing each other. I randomize these groups so that a group of three is together at most for five classes. I write problem sets that dip into past knowledge and ask some questions for which we have not been explicitly prepared. My quizzes are narrowly focused on recent information and they are weighted less than tests. My tests are all cumulative in nature but they are about 70% focused on what has happened since the last test. I want at least one test question to feel novel, to ask students to put together information in a way that feels new – a problem rather than an exercise, I guess I’d say. We have a test correction policy that we adopted this year (you can read about that here, here, and here ) and this policy seems to have helped reduce anxiety a good bit. All of this is to provide a little context into my classroom and my vision of what these phrases ‘Be Less Helpful’ and ‘Becoming the Math teacher You Wish You’d Had’ mean.
What I have struggled with, this year more than in the recent past, is the discrepancy between the math teacher I wish I’d had and the math teacher that my current students wish they had. A good number of my students seem to be happy wth how our classes run. I have posted a number of entries this year about student success. I have received some lovely emails from parents of students in Geometry, some nice remarks passed along from colleagues about students in Calculus Honors, some terrific conversations with students in Discrete Math, and an abundance of energy and creativity from my AP Calculus BC gang. In all four of my classes I feel I am reaching some students and making a positive impact. What concerns me, and what prompts this post, is the fact that a number of students are not buying what I am selling. They are frustrated when I respond to a question with a question. They think it is unfair to have a test question that does not look like something they have explicitly practiced. They feel that I am off loading my responsibility as the teacher when I ask them to work in groups to figure something out instead of lecturing and telling them how to figure it out. I have students across a wide range of abilities and a wide range of reactions to what I am trying to accomplish. It is important that I recognize this and do not simply bask in the glow of the students for whom this approach really clicks. Where I struggle, is trying to reconcile what I think I understand about teaching research, what I understand about NCTM’s recommendations, and what I valued as a student with the discomfort and unhappiness that I see in some of my students. I also struggle with balancing what is clearly working with some students in each subject. I don’t want to lose that energy and motivation that I see in students who value what feels like a different way to experience math. I know that this is not an either/or situation. I have two weeks of spring break to think and reflect. I know that there is a way to reach the frustrated kids without giving up the the facets of my class that are valuable to some of their colleagues (and to me!), I know that there is a balance to be struck between asking kids to step out and feel challenged and making sure that they still feel supported.
I think back to a comment from a student abut 6 years ago. About three weeks into the school year she asked for a personal conference to talk about her struggle in our Honors Calculus class. By the way, struggle for her meant that she had a B average instead of her typical A. She said to me ‘I thought that I needed to learn formulas and how to use them. That isn’t working here.’ She and I had a lovely conversation and in the years since I have run into her dad a number of times. He always tells me how important my class was for his daughter. She has sent me lovely thank you notes updating me on her progress. She is an example of a student I was able to help cross a certain threshold. I want that feeling for all of my students in some way or another and I have solid evidence that this is not happening often enough right now. I have some serious thinking to do.
Vocabulary
This post is inspired by a twitter exchange with the awesome Joe Schwartz (@JSchwartz10a) and by a running exchange with one of my Geometry students. Joe tweeted out the following picture: 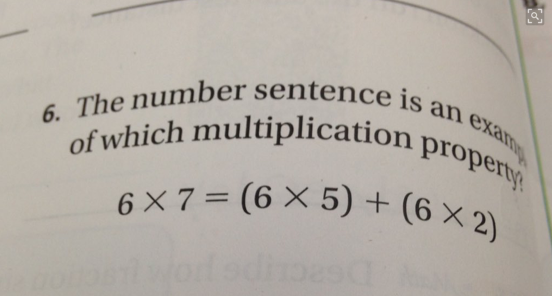
The picture was accompanied by the question : “Do 3rd graders know the answer to this question? Truly curious.” It just so happens that my Lil Dardy is in 3rd grade. I showed her the question and (briefly) explained the equation written. I replied to Joe that she was not surprised to see it written that seven sixes is the same a five sixes plus two more. However, she did not know any vocabulary word to describe this. Joe replied, succinctly, “And she doesn’t need one…” It made me smile. It also made me think when I was reviewing for a test with one of my Geometry classes. We just finished a chapter on triangle bisectors and centers. Loads of vocab in this chapter. Very few new skills, just new words describing relationships. Thinking back to the exchange with Joe I found myself questioning my decisions in writing the book and in teaching this chapter. During the test review a student asked if there would be any vocabulary on the test. This particular student has asked this question before just about every test. I answered the way I do just about every time. I told him that he needed to know what these words mean to accurately interpret the questions at hand. For example, if I ask about altitudes to a triangle, he needs to know what that means. However, there would not be a question where I simply ask him to replicate the definition of an altitude. Thinking back on this exchange, and this way that I answer the question, I have a ton of questions that I need to ask myself and I will start by posing some of them my readers out there.
- My guess (an uncharitable one) is that the student asking about vocabulary is looking to avoid committing anything formal to his short term memory before a test. Admirable in a certain way, but what does this question say about what he thinks his job on a test is? Why would students who have been working with words day after day express any serious concern about being asked what those words mean?
- Real people have real vocabulary that they use in their studies, in their work environment, etc. I recoil at the suggestion that I should do something objectionable now because someone will do it to my students later. But, I am beginning to wonder whether I am cheating my students a bit. Should I be more emphatic in urging them to be careful about vocabulary now so that they will better understand what they read or hear later? Am I being lazy when I let them casually refer to the longest side of any triangle as the hypotenuse? [Note: I have written about this before. I DO correct them, but in a pretty gentle, nudging way. I remind them every time that the hypotenuse is a specific name, but this habit has settled in with my students for a couple of years now.]
- What are we communicating to our math students if we mark points off or hold them accountable in some ways to formal language if they can get their mathematical ideas across through their work? Are these skills dependent upon one another? Is it okay that my students can swing into action and write the equation of an altitude of a triangle but be uncomfortable and vague if asked to write a definition for what an altitude of a triangle is? As someone who is so comfortable with these words, I struggle to understand how someone can write that line without being comfortable that they can write a definition, but I’ve been teaching long enough to know that this is a real thing.
- Is this another instance where students have been trained to think that there is one right way to answer a question and their job is to make sure that they simply regurgitate (if they can decode correctly) what that correct answer is. I, of course, hope that my grading policies and the way that I communicate in class convinces my students that this is not the way life is in my classroom. However, I know that I am battling impressions that have formed over years.
- More importantly – Does it matter that my students know things like the altitudes of a triangle intersect at the orthocenter? Is there ANY chance that they will remember this in a few months? In the past few years I taught the course, I pretty much only mentioned the word centroid and avoided talking about incenters, circumcenters, and orthocenters. I am not at all sure that I made the right decision then or that I made the right decision this year in explicitly defining them. In my text the words centroid and incenter are explicitly defined. Circumcenter and orthocenter do not even appear in the text. A mistake then? A mistake now? I’d love to hear some advice/opinions.
Gotta get dressed for school now. More thoughts swirling and I hope I am disciplined enough to get them down soon.
Thanks to Joe for prompting this post!
As always, you can reach me here in the comments section or over on twitter where I am @mrdardy