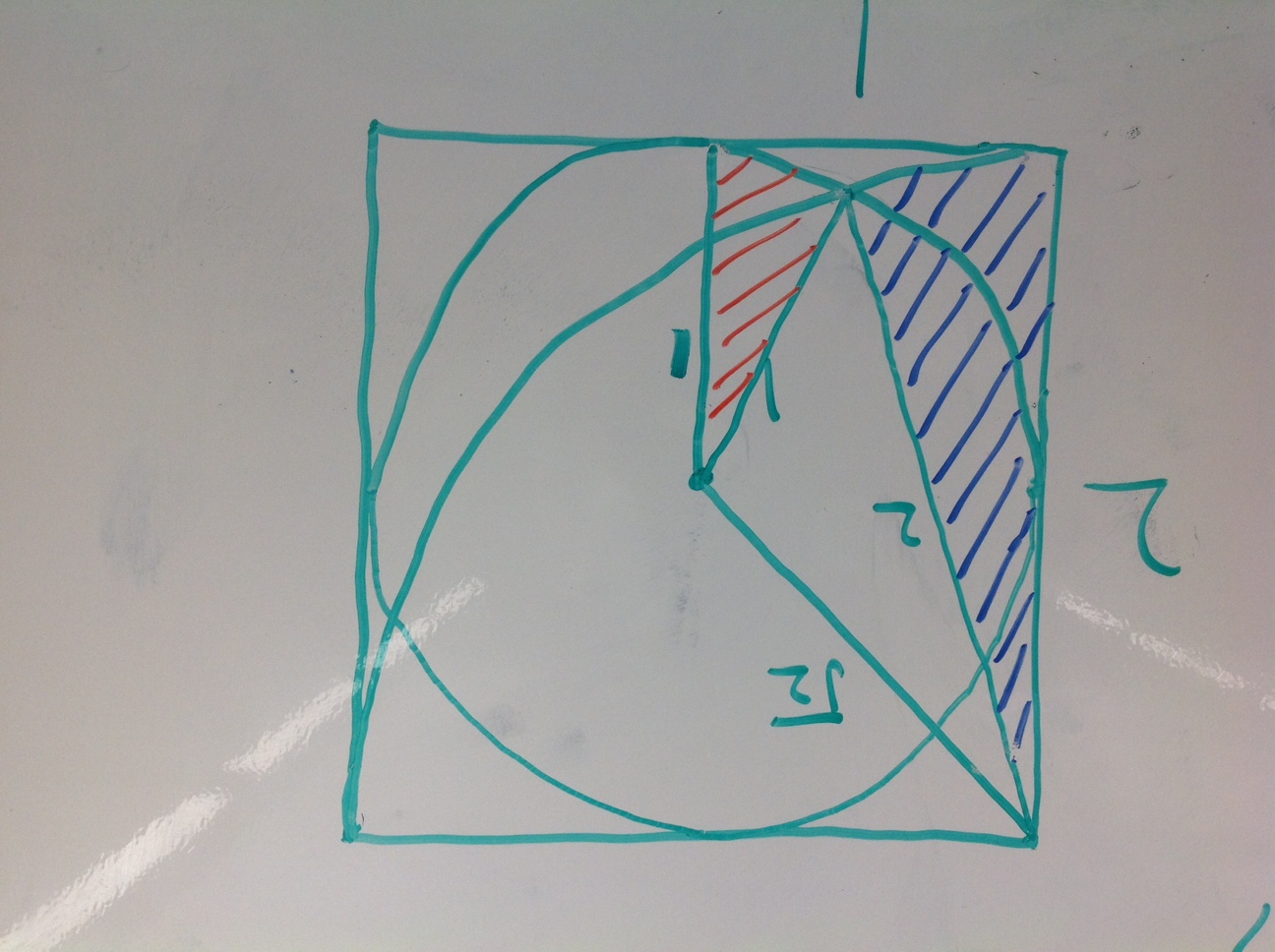
Last week – I know, it’s taken too long to write about this – my Precalculus Honors class started the day with a brief quiz. One of my PCH students named Max finished the quiz early and started sketching on his scrap paper. He showed me a diagram like this:
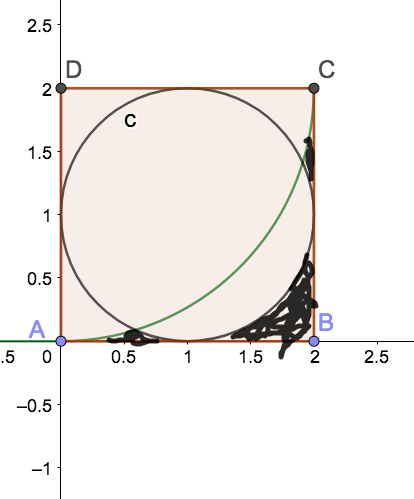
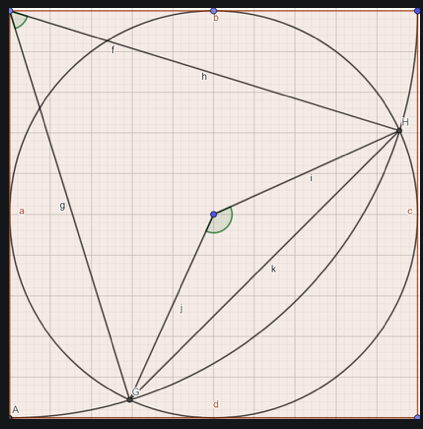
He described the problem this way – I have a square and a quarter circle coming across it. I also have a circle inscribed in the square. What is the area of these little regions? (I clumsily sketched in those regions on GeoGebra)
Well, it turns out the the topic of the day in AP Calculus BC that day was to be trigonometric substitution for integrals and this problem would be a lovely introduction to the need for this skill. AP BC was meeting for the 90 minute block and I decided that I would introduce Max’s problem, spend about ten minutes dissecting what we could and then hit a bit of a wall where I would introduce this new skill. I was pretty proud of myself and feeling very fortunate that Max thought of this question. Well, as we all know, life doesn’t always work out the way we want it to in school. I presented this problem and told them that it came up in Precalculus Honors. My BC kiddos started dissecting it right away. They concentrated on the lower left corner, they decided we should agree to a side length for the square and off they went. We decided the square should have a side length of 2 so the inscribed circle would have a radius of 1. Avoiding fractions until we HAVE to deal with them is a good plan in general, right? So, the lower region is 1/4 of the difference between the inscribed circle’s area of pi and the square’s area of 4. Good start. Next we convinced ourselves that the two remaining squiggly areas are congruent. It would have been nice if we could drop a line from the point of intersection to divide that region in two but it’s not symmetric. The different radii of the circles intersecting prevents that from being true. So, here is where I figured I would introduce this new technique. I mentioned this idea but the feeling in the room was that we should be able to answer this question using tools that a precalc student should be able to use. I was sitting in the back of the room at this point with my laptop on and a GeoGebra sketch projected on the front wall. Ideas and questions started flowing and students asked for a Desmos sketch like the one below:
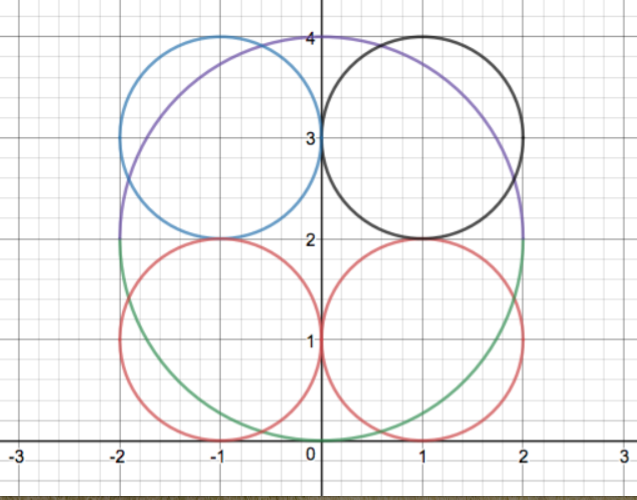
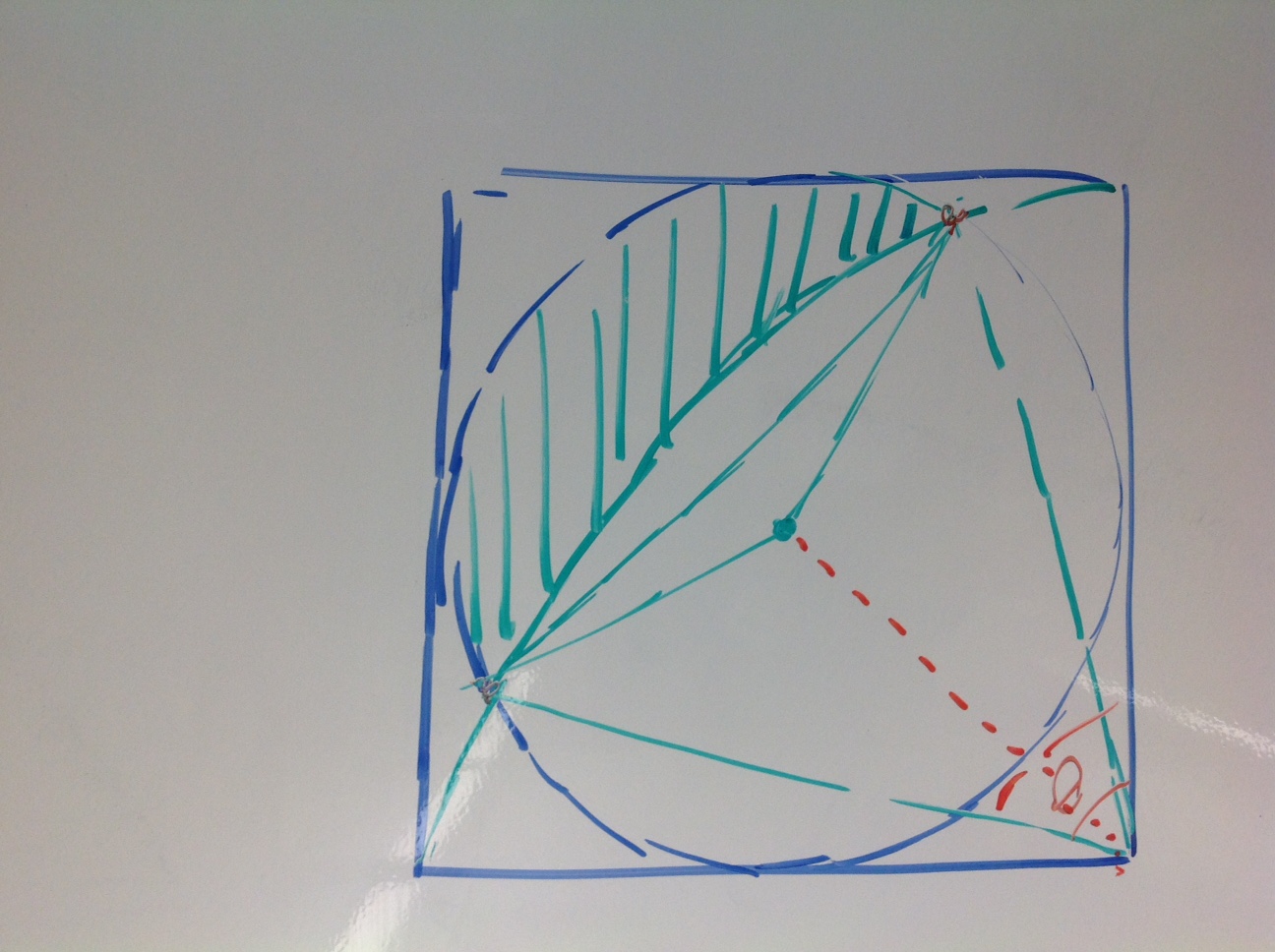
Jake proposed this and felt that the added symmetries would be helpful in discussing this problem. I asked if anyone wanted to see a point of intersection identified and we did at first but then erased that point from the conversation. We are about 20 minutes into our 90 minute class now and probably at least 5 minutes behind where I wanted to be but the energy in the room was pretty incredible. Students started going up to different boards and sketching ideas. They asked for paper printouts of the demos sketch and started moving from small table group to table group. People were debating and correcting each other and I just sat there. I was listening, I was tossing out questions, but mostly I was just watching this all unfold. The students were dusting off old trig ideas and old geometry ideas. They were debating the need/desire to have the decimal guess of the point of intersection. One student, Nick, was determined to think about this in terms of proportions and he drew a lovely argument that the area would end up being around 10% of the whole square. His classmates were unconvinced and he argued his point two or three different ways. One student, Colin, broke the region into circular arcs and argued about finding the area of a central angle. He had a great drawing but I did not capture it on my iPad. This conversation kept rambling on over the course of our allotted 90 minutes together. I proposed a couple of times that I could give them a new calculus tool but they kept waiving me off. Noon rolled around and I told them they could go to lunch. Many of them did, kind of exhausted by all of this at that point. One group of three – Nancy, Andy, and Michael – were fired up at this point and were sure that Colin had made some small mistake in his sketch. They produced this –
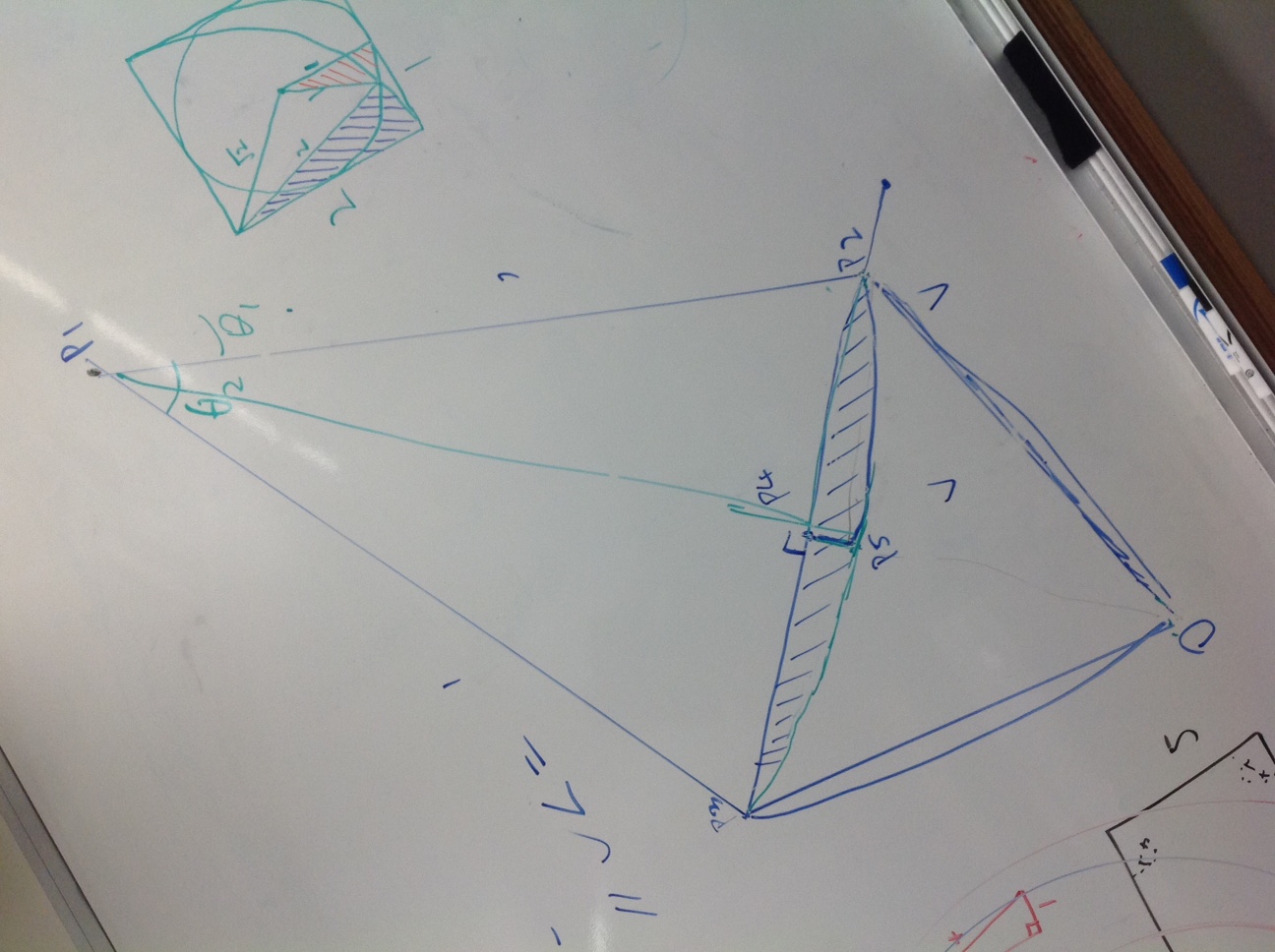
So, this sketch is pretty impressive in its detail but, more importantly, this sketch happened about 20 minutes after lunch began and after I excused myself to run an errand during lunch. During the 90 minute class, my colleague David from across the hall wandered in a couple of times asking kids to explain what they were doing. He told me that Nancy, Andy, and Michael worked for at least a half an hour of they hour long lunch debating this problem. The other thing that happened while I was gone was that Andy, Kelly, and Michael had modified my Desmos sketch on my laptop pursuing their idea. Their modification is here –
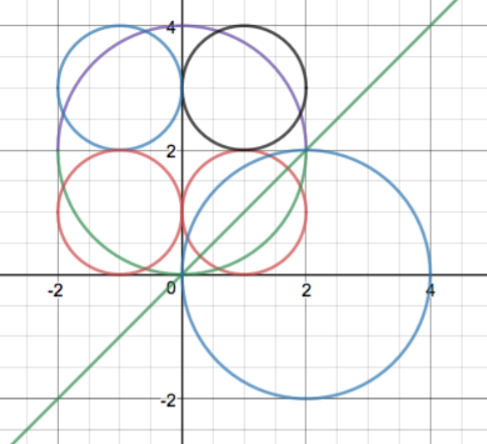
I was feeling pretty great about their perseverance, their engagement, and the amount of geometry and trig that was being remembered in the service of this curious problem proposed by one of my students. I was also more than happy to amend this week’s Calc test by taking off the one problem that relied on the trig substitution technique. I had one more class after lunch (one of my Honors Calculus sections) so I sadly erased some of the work on the board and I described the problem to that group. Some of them had already heard about it during lunch! My BC kiddos were still talking about it even after they left. At the end of the day one of our Differential Equations students wandered into my room. He said ‘I heard there was a good problem today.’ He, Owen, then proceeded to discuss the problem with Andy and Nancy who had come back to the room to discuss this. Owen dove in to the problem debating with Andy and Kelly and he produced these sketches – (the first one got rotated in translation)
I tweeted the problem out, like I do, and a former student jumped in and offered this sketch –
Another colleague, Adam, came by when he overheard this conversation and he attacked the problem using Google sketch up to find the ratio that Nick wanted – it was smaller than his proposed 10% neighborhood.
There is no real ending to this story, the weekend came, life moved on. On Monday my BC class was more focused on asking questions about this week’s test. My Precalc Honors kids were impressed by my enthusiasm in talking about all of this but they did not share Max’s curiosity about the question. I went home feeling pretty great about the sense of play and sense of curiosity of many of my students and my colleagues. While I cannot let everyday roll this way, I need (NEED!) to make sure to create spaces where this kind of magic can happen. I think almost all of the credit for this adventure lies with my students who are interested, motivated, curious, and persistent. I hope that I have helped them along by modeling curiosity and by being willing to let this kind of free range play happen in class.