Category: Geometry

Persistence and Patience

Neither of the qualities in the title of this post are apparent in abundance at this time of the school year (exams here start on May 21!!!) so I am especially pleased to be able to write about today in my two Geometry classes. They each took a quiz with me in their last class and I asked them to read ahead to the next section (more on that later) before meeting again today. After a brief warm up we reviewed the quiz and I returned papers. Then I presented them with this image from our Geometry text

 

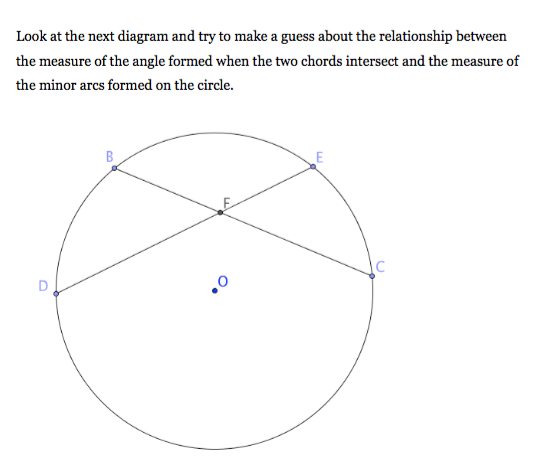
Now, at this point we have established that the measure of a central angle in degrees is equal to the measure of its intercepted arc in degrees. We have proven that the measure of an inscribed angle in degrees is half of the measure of its intercepted arc in degrees. I told them that my dream for today was to derive some formula relating the measure of angle EFC to some combination of the arcs BE, EC, CD, and DB. I reminded them of what we already know and suggested that using what we already know is often pretty helpful when trying to learn something new. I then stepped back and let kids toss out ideas. In one of the two classes I took a walk to the water fountain and popped in on a colleague for a two minute chat. I came back into a room with people debating and waving their hands in the air to show what segments they wanted to draw. I wish I saw more drawing at their desks, but it was good engagement. In both classes they wanted me to name the vertical angle pairs at the hinge point F. I was a bit surprised that neither group wanted to name arcs yet, but it worked out just fine. I dropped a hint that another segment drawn would help and this spurred some lively debate about what segments to draw. BE and DC were popular but I pointed out that the vertical angles were not included really in these triangles that were formed. Some folks wanted some radii drawn. One girl was sad when we named our vertical angle pairs. She saw that BFE and DFC were clearly equal but that they faced arcs that clearly weren’t. I was pleased by this observation. There was a real desire in each class to assume that BD and EC were equal and I wish my diagram was more clearly designed to discourage that. We finally settled on drawing the chord BD which created two inscribed angles that we called x and y creating arcs called 2x and 2y. The heavy lifting and guessing were done by that point. Arriving at the conclusion that we now need a relationship between one angle and two arcs came in a couple of steps. In both classes I made a clear statement about what we just discovered and they seemed pretty pleased with themselves, if a bit tired from the exertion. In my morning class we were on our 90 minute block and I gave them some practice exercises that we will revisit tomorrow. In my afternoon class that ended the day we simply left the discovery on the board. I start tomorrow morning with that crew and I am excited to pick this up again.

In each of my classes I have 14 students. One was absent today, so I had 27 overall joining in on this conversation. One of them, when I mentioned my dream for the day, said ‘In the reading last night it said that this angle is the average of two arcs.’ [Thank you Niko!]

One student. Now, it is entirely possible that other students did the reading I requested. It is possible that some read the section and were confused by it. It is possible that some read it and forgot the conclusion. It is possible that some who read it simply did not feel like saying anything out loud. It feels more likely that few (maybe only 1?!?) did the reading.

I could dwell on that, but I am dwelling on the discovery we made. I am dwelling on the persistence and patience of my students today. I am dwelling on what went right to end a day that started poorly for me.

 

Later, I’ll dwell on how I can help overcome the likely habits of not reading that I am faced with. I’ll save that for a less beautiful day than today.

Vocabulary

This post is inspired by a twitter exchange with the awesome Joe Schwartz (@JSchwartz10a) and by a running exchange with one of my Geometry students. Joe tweeted out the following picture: 

The picture was accompanied by the question : “Do 3rd graders know the answer to this question? Truly curious.” It just so happens that my Lil Dardy is in 3rd grade. I showed her the question and (briefly) explained the equation written. I replied to Joe that she was not surprised to see it written that seven sixes is the same a five sixes plus two more. However, she did not know any vocabulary word to describe this. Joe replied, succinctly, “And she doesn’t need one…” It made me smile. It also made me think when I was reviewing for a test with one of my Geometry classes. We just finished a chapter on triangle bisectors and centers. Loads of vocab in this chapter. Very few new skills, just new words describing relationships. Thinking back to the exchange with Joe I found myself questioning my decisions in writing the book and in teaching this chapter. During the test review a student asked if there would be any vocabulary on the test. This particular student has asked this question before just about every test. I answered the way I do just about every time. I told him that he needed to know what these words mean to accurately interpret the questions at hand. For example, if I ask about altitudes to a triangle, he needs to know what that means. However, there would not be a question where I simply ask him to replicate the definition of an altitude. Thinking back on this exchange, and this way that I answer the question, I have a ton of questions that I need to ask myself and I will start by posing some of them  my readers out there.

  • My guess (an uncharitable one) is that the student asking about vocabulary is looking to avoid committing anything formal to his short term memory before a test. Admirable in a certain way, but what does this question say about what he thinks his job on a test is? Why would students who have been working with words day after day express any serious concern about being asked what those words mean?
  • Real people have real vocabulary that they use in their studies, in their work environment, etc. I recoil at the suggestion that I should do something objectionable now because someone will do it to my students later. But, I am beginning to wonder whether I am cheating my students a bit. Should I be more emphatic in urging them to be careful about vocabulary now so that they will better understand what they read or hear later? Am I being lazy when I let them casually refer to the longest side of any triangle as the hypotenuse? [Note: I have written about this before. I DO correct them, but in a pretty gentle, nudging way. I remind them every time that the hypotenuse is a specific name, but this habit has settled in with my students for a couple of years now.]
  • What are we communicating to our math students if we mark points off or hold them accountable in some ways to formal language if they can get their mathematical ideas across through their work? Are these skills dependent upon one another? Is it okay that my students can swing into action and write the equation of an altitude of a triangle but be uncomfortable and vague if asked to write a definition for what an altitude of a triangle is? As someone who is so comfortable with these words, I struggle to understand how someone can write that line without being comfortable that they can write a definition, but I’ve been teaching long enough to know that this is a real thing.
  • Is this another instance where students have been trained to think that there is one right way to answer a question and their job is to make sure that they simply regurgitate (if they can decode correctly) what that correct answer is. I, of course, hope that my grading policies and the way that I communicate in class convinces my students that this is not the way life is in my classroom. However, I know that I am battling impressions that have formed over years.
  • More importantly – Does it matter that my students know things like the altitudes of a triangle intersect at the orthocenter? Is there ANY chance that they will remember this in a few months? In the past few years I taught the course, I pretty much only mentioned the word centroid and avoided talking about incenters, circumcenters, and orthocenters. I am not at all sure that I made the right decision then or that I made the right decision this year in explicitly defining them. In my text the words centroid and incenter are explicitly defined. Circumcenter and orthocenter do not even appear in the text. A mistake then? A mistake now? I’d love to hear some advice/opinions.

Gotta get dressed for school now. More thoughts swirling and I hope I am disciplined enough to get them down soon.

Thanks to Joe for prompting this post!

As always, you can reach me here in the comments section or over on twitter where I am @mrdardy

A Tale of Two Questions

This past week I had a quiz for each of my Geometry sections. The two sections are out of synch a bit due to our rotating schedule. They typically assess on different days with different versions of whatever quiz or test I recently wrote. This week’s quiz had two different forms of the final question. I present them below:

In the diagram below you see a triangle ABC and you see what are called the exterior angles of the triangle marked. What is the sum of the measures these exterior angles? Be careful to carefully show your reasoning. Mark any angles clearly that you want to refer to in your explanation.  

The problem above was presented to my class on Thursday.

In the diagram below you see a triangle ABC and you see what are called the exterior angles of the triangle marked. The sum of these exterior angles is 3600. Write a proof explaining to me why this is true. Mark any angles on the diagram that you refer to in your proof.

The problem above was presented to my class on Friday.

Both classes had the same first problem on their quiz. They were asked to prove that the interior angles of a triangle sum to 180 degrees. This proof was explicitly presented in class and in their text. My thought was that this challenging fifth problem should be a (somewhat) natural consequence of the first problem on the quiz.

The students who took the quiz on Thursday struggled on the first problem and it bled over to the last. They generally performed better on the last problem than on the first. In part, this is due to my decisions about partial credit. I was definitely more generous with partial credit on the problem at the end of the quiz since they had not seen any explicit proof of this fact. My colleague who also teaches Geometry felt that I might be reaching a bit with this last question. My Friday class performed better on the first proof than the Thursday crew and they did a MUCH better job on the last problem. I am trying to sort this out and there are too many variables at play. First, the class who took the quiz on Friday has performed at a slightly, but consistently, higher level overall during the first trimester of our year. Second,there is always the possibility that information about the quiz was discussed in a way that gave the Friday class some advantage. Finally, the problem presented to them gave an answer and asked for justification while the problem as presented to the Thursday class did not provide the conclusion. I was more strict with partial credit with the Friday quiz class since the conclusion was given to them and the whole burden of the problem was the explanation.

The main reason I am writing about this is that I am trying to make myself think clearly about what my goals are in a  problem like this one and to convince myself that I was trying to get at the same thing with both classes. Did I drastically change the nature of what was being assessed by presenting the conclusion already? I have thought out loud on this blogspace about a similar question here – https://mrdardy.mtbos.org/2017/09/22/a-quick-question-about-test-questions/

Did revealing the answer to the question fundamentally change the level of challenge inherent in the question? Is it THAT much easier to reason through the proof when you know what you are supposed to conclude?

Our Geometry course is the last course in our curriculum where there is no Honors option. Everyone who takes geometry takes the same course at our school. This means that there is a wider variety of interest and talent in this room than in my other classes. I think that there is a tendency in a non-honors math class to think that the students cannot tackle challenging or novel questions. I have heard several colleagues over the years say something along the lines of ‘I can’t ask that question if I haven’t shown them how to do it.’ These are terrific teachers saying this and they are coming from a good place, they want their students to succeed and they do not want them discouraged or dismayed by assessments. I think I am coming from a good place as well, it’s just a different place. I’d also say that in the case of the question above, especially in its first form, I do believe that I have shown my students how to tackle such a question. They know that the interior angles sum to 180 degrees. They see three supplementary pairs of angles so that sum is 540 degrees. The difference is the exterior angles. Half of the students in the Thursday group earned four or five points out of five on the problem. Those who earned four generally had sound logic with real flaws in the vocabulary explaining their answers. Maybe my docking them a point is an entirely different question about how I assess.

Another reason I am writing this is that I want to have a conversation with my department about questions like this one, questions that are not a simple transformation of what has already been practiced. I have students who imply that I am the first teacher they have who asks them questions that feel like they might be ‘from left field.’ I know that students (all people, really) will exaggerate their concerns in the face of feeling stressed. I think most of my students do a nice job of stepping up to challenges like this one, especially when points are riding on it on an assessment. But I also know that there is an instinct at times to simply dodge these situations. The same group of kids who took the quiz on Thursday were presented with a problem from Steve Wyborney’s website on Friday in class. I showed them the video of the duplicator lab problem.  When the video ended I asked them to begin talking about the problem with their neighbors – in this class everyone sits in groups of three that get randomly reassigned every fifth day. I was met with mostly silence. To be fair, this was about 8:10 in the morning. However, when I showed them the comments section with teachers talking about their fourth and fifth graders solving the problem, they suddenly started talking. So, I don’t know if they were shamed into action or they simply needed to suspect that they were more than capable of solving the problem before they moved. I have to feel that the struggle with the problem on Thursday and their reluctance to engage with a novel problem on Friday morning are related. I also fear that I have not done enough yet to create a culture where they jump into these problems. I am interested in how the conversation goes with my department on Wednesday morning and I would love to hear from any readers as well.

 

Back in the Saddle

I gave myself the month of June off after a busy year. On July 2 I sat down and started a project that I was stewing about all year long. I am happy about the problem sets I wrote for Geometry, I think that they are a nice set of interesting problems. Many of them have been borrowed from sources all over the internet and I think that my students who took them seriously are more persistent in their problem – solving than they were when the year began. However, I also learned a couple of important things along the way. Not all of my students gained in persistence through these problem sets. In part, I think that the students found them a bit intimidating at times. I also think that they skewed a little long on time needed for thoughtful reflection. I have two solution ideas for the upcoming year. We purchased a license to Kuta’s Infinite Geometry (and their other course options) and I did not use this as often as I should have last year. I do not think that these are terribly thoughtful exercises, but I do know that they are flexible (for me) and supportive (for my students) and I need to use them more often. Since all of our classes in our new schedule are at least 50 minutes, I will be able to carve out comfortable space for in-class practice on basic skills as we are developing them. I also made a commitment to reviewing my problem sets and working on two improvements. I wanted to clean up the language and make sure that problems are a bit clearer in what I want my students to focus on. I got engaged in a great twitter conversation about how important it might be to have students answer y-intercept questions as ordered pairs rather than as a number and how important it is to talk about the graph of a line as an object that is distinct from the equation of a line. I tried to make sure I talked about points on the graph of the line whose equation is 2x + 3y = 12 instead of asking for a point on the line 2x + 3y = 12. Just one example of how I tried to clean up the language I was using. More importantly, I trimmed many of the problem sets by eliminating some questions. I have posted all of my HW problem sets on my dropbox and I am happy to share them with anyone who wants to borrow (or just outright steal!) from them. You can find those problem sets here.

I would love to hear any advice/questions/concerns about these HW assignments. Please reach out by commenting here or through twitter where I am @mrdardy

 

Trying to Help My Students Help Themselves

Years ago, I ran across a calculus document by a teacher and AP grader named Dave Slocum. He called his document How to Succeed in Calculus and gave it as a handout at the beginning of the year. I modified it and used it as an intro document when I was teaching AP Calculus AB for years. Last summer I modified it for use with my Geometry kiddos. As many of you know I wrote a text for Geometry that we use at our school. If you are interested in it, you can find it here. In the last two years using this text I realized (remembered?) that these younger students don’t always have the same good habits that my AP students have. So, I created a document called How to Succeed in Geometry (you can grab it from the link) and shared this with all of my students and their parents. I revisited this document two or three times in the first month of the year. I am realizing now that this is not enough. If I am serious about supporting my students and helping them develop positive habits, I need to revisit this over and over again in the early part of the year. I stopped doing so for a number of reasons and none of them are valid enough. I don’t like to read to my students, I know that they can read. However, I should also know that many of them will not read a document like this one. I stopped revisiting it because I was getting frustrated by saying the same things repeatedly about classroom behavior. This is not a good reason. I need to be more patient and realize that all of the teachers that they have during the day have different expectations. I need to remind them of my expectations, just like I need to remind my children at home to do their chores or to put dishes in the sink. I think that the difference is that I am more willing with my own children to be a nag. I am more confident that I have built up a decent reservoir of good will with them. Early in the school year, I do not have that sort of reservoir with my students. The reason I am writing this now is that I sort of snapped with my Geometry students last week after a particularly disappointing set of quizzes. The mistakes made on this quiz made it abundantly clear to me that many of my students were not taking my advice about how to succeed in this class. One student said out loud, somewhat dejectedly, that he wants to succeed. Without changing behaviors, it is hard to take a statement like that one as being particularly meaningful. If I genuinely want to be healthier and more fit, I need to change behaviors to make this happen. If my students genuinely want to succeed, they need to be willing to change some behaviors so that this is more likely to occur. I know that I want them to succeed and that is one of the reasons why I prepared the document that I did. I just need to be far more committed to using that as a breathing document next year and not wait until the last week of April to mention this for the first time since September.

I’d love to hear any words of advice about reinforcing these habits of work and habits of mind. You can drop comments here or over on twitter where I remain @mrdardy

My Students are Making Some Smart Guesses

On Friday in Geometry we were continuing our conversation about triangle centers and I asked my students to find the point where medians coincide in a scalene triangle. There is a good amount of algebraic detail in these problems but my students were doing a nice job pushing through this problem. After finding the centroid, I asked them to form a new triangle from the three midpoints we needed when considering medians. We found the perimeter of the original triangle and I asked also for the perimeter of the triangle formed by the midpoints. One of my students theorized that the new triangle would have one-fourth the perimeter of the original triangle. I asked the other students to quiet for a moment to hear this guess. Before asking GeoGebra to check his answer he quickly corrected himself and said he was thinking about area, not perimeter. A beautiful realization on his part that this triangle formed by midpoints would divide the original triangle into four equal areas. Just as we were congratulating him for this guess another students asked about equilateral triangles. He wondered aloud whether the midpoint triangle in an equilateral triangle would form four equilateral triangles. I realized he was asking whether the triangles formed in the scalene we were looking at were also congruent, not just equal in area. A quick question from me confirmed my guess so we drew our attention again to the GeoGebra sketch we had up. He was able to identify where the congruent angles were that allowed us to prove congruence for the triangles.

This conversation was a wonderful way to end our day on Friday. I am delighted that my students are comfortable enough to make these guesses out loud and even more delighted that they are making such good guesses right now. I pointed out how helpful it is to play with GeoGebra to check these guesses and I hope (I hope hope hope!) that some of my students are making a habit of this.

A Delightful Conversation

Last week in my Geometry class we had a fantastic conversation about a homework problem. Here is the problem in question –

screen-shot-2016-12-06-at-3-56-52-pm

 

I wish that I could take credit for having written this, but I am certain that I ‘borrowed’ it from somewhere. Likely from the fantastic resources shared with me by Carmel Schettino (@SchettinoPBL)

So, this is the kind of problem that I expect only a minority of my students to navigate successfully on their own, but I am convinced that almost all of them will benefit from thinking about a problem like this one, from a little active struggle along the way. I KNEW that this would be asked in class if anyone took the time to do the HW I assigned, so I was pleased that it came up. I started by telling my students that I LOVE this problem and asked them if they could guess why. One student said ‘Because it’s so hard’. I laughed that off and said, yes it is hard but I love it because it ties together a bunch of important ideas. Off we went on solving this. I started by asking a couple of questions that probably seemed a bit irrelevant at first. I asked why they knew that the y-intercept was (0, 3) and that the x-intercept was (4, 0). Before they could answer I made sure to mention that they knew this without looking at the graph. We eventually arrived at the realization that we know whether a point is on the line or not by looking at the equation itself. If a point makes the equation true, then that point is on the line. If not, then not. This is the kind of thing that I think my students know but being reminded regularly sure does help reinforce it. I hope! So, I thought I had set the hook here for the rest of the problem. We talked about what we know about squares and we talked about how to identify points on the square without knowing their real coordinates. We got a little lazy, and I was okay with that,by calling the bottom right corner (x, 0) and the top left corner (0, y). This gave us no choice but to call the top right corner of the box (x, y). At this point I paused and asked them to remind me what needs to be true about points on a line. Then I asked them to remind me of what we know about a square, therefore what we know about x and y for that mystery point (x, y). It wasn’t easy to get everyone to agree with our conclusions, but I think we got there. We agreed that the x and the y had to equal each other. We agreed that the y coordinate had a definition based on x. We agreed that this was an equation we could solve even though it was not a bunch of fun to solve it. After all of this work it felt like the problem should be done, students were pretty sad to realize it wasn’t. We still had a conclusion to make about the triangles created. One of my students was pretty insistent that they needed to be congruent because their angles had to match up. This was not the time to launch into a conversation about similarity and I decided it was not the time to talk about the restrictions of AAA conclusions between triangles. We have talked about equilateral triangles of different sizes and we are (mostly) okay with that, but I felt that that conversation would be a diversion here. Instead, we kept at the calculating and we looked at side lengths. Once we agreed that they were not congruent, I pointed to the slope of the line and talked about the fact that his instinct was foiled by the fact that x and y lengths were not changing at the same rate. The whole conversation took quite some time, might have been 15 minutes by the time the whole thing was done, but I felt that we had done some important heavy lifting.

If you recognize the above problem as your own, feel free to claim it and let me know. Know in advance that I am very grateful for such a rich problem to tie together ideas of distances, slopes, line equations, properties of squares, and triangle congruencies all into one tidy package!

 

Hands-On Geometry

I’ve been at this high school math gig for a good long while now but I periodically have to remind myself of a couple of important facts. The most important one is that not everybody’s mind works like mine. Just because I like a certain way of thinking, or dislike a certain way of learning, I should not assume all my students will agree. In fact, I can be pretty certain that all of my students will not agree, there’s too many individuals for that to work.

When I studied Geometry I did not like physical drawings and constructions. In part because I am a bit inept when it comes to controlling something like a compass, but also because getting my hands engaged does not seem to fire too many of my neurons. So, when I wrote my Geometry book a couple of years ago I did not include much in the way of hands-on manipulations. The past couple of years of working through the text with our students has pointed out the weakness of this approach. So, I put my head together with one of my talented colleagues to try and make an activity that would trigger some neurons for those students who come to life when they get their hands busy. I had been using a pretty cool activity I ran across from Jennifer Silverman but I made pretty flimsy paper copies to work with on a pipe building activity where kids had to manipulate bent angle joints with different pipe lengths. It’s a great activity but using simple paper copies dragged the activity down. We invested in some packs of AngLegs this year and my colleague wrote a pretty cool activity modeled off of our pipe building activity. You can find his document here.

I was impressed as each of the seat groups in my class played with the AngLegs making some discoveries about combinations that worked and those that would not. We discussed, without naming it yet, the triangle inequality theorem to explain why some combos did not work. But the real fun, and the clever heart of my colleague’s activity, was when I asked one student from each group to come to the front of the room. When they left their group the remaining group members were given the following task – I slightly modified the original document on the fly – I asked them to make and measure a triangle. Find six measures, the three side lengths and the three angles. They then put the triangle away where it could not be seen. I sent the volunteers back and their teammate gave them three pieces of information. I left it to each group to decide what information to share. Once given three clues the volunteer student needed to manipulate the AngLegs to copy the triangle described. What ensued was a terrific conversation about what information is necessary to guarantee that I have to make the same triangle. We used this as a launching pad to discuss congruence theorems for triangles. I have some great links in the text to some wonderful GeoGebra activities up on the GeoGebraTube site but I know that many of my students do not do these explorations.  I also know that some just need to get their hands dirty, so to speak. Some kids were able to recreate the triangle but admitted that it was a bit of luck. Some stumbled upon the ambiguous case of the Law of Sines without being told that this is what happened. Some realized that they had no choice but to create the correct triangle.

I was really pleased by the level of engagement and I am now thinking about ways to use the AngLeg sets again soon when we start talking about side and angle bisectors. I want to have tables create and draw their own triangles before we stumble into discoveries about concurrence of these bisectors. This will feel, I hope, a little more authentic than me just giving them a prescribed triangle which may feel a bit like I am just luring them into some pre-prepared trap. I think that this activity we ran benefited my students and we have referred to it on a number of occasions already. The grouping of three or four students together at a time helps and allowing them to get their hands busy has helped. Looking forward to loosening up a bit more and letting my students be more tactile in their approach to Geometry. I’ll still show them the GeoGebra and introduce them to Euclid the Game  but I need to remind myself that they are not a bunch of mini Dardys in the room.