Month: October 2019

Problem Sets

For quite a while now I have been writing problem sets for my AP Calculus BC students. I scour old books, math competition files I have, problem sets from Exeter and other schools. I cobble together odd, open ended sets of problems intended to give my students the opportunity to grapple with novel problems in a manageable time frame. I encourage the students to confer with each other, to talk to me, to play with GeoGebra, Desmos, WolframAlpha, etc. In a way this is intended as a grade buffer, but mostly it is a way to get them to play with fun students. This year, I am also writing problem sets for my Calculus Honors and Precalculus Honors students. I want to write about something cool that some of my Precalc Honors kiddos presented. Here is the question I presented:

  1. Consider the graph of the function f(x) = 5/x  from the point (1,5) to the point (5,1). Explain a way to approximate the length of the curve between these points and arrive at some numerical approximation. You can describe your process in words, with a graph, or a combination of the two.

Now, my goal with this is to prime the pump for important calculus notions of infinite sums, Riemann sums, etc. I hoped that some students would suggest plotting a couple of points along the curve and adding the distances. One student in particular kept pressing me on this question which, admittedly, is probably more open-ended and formless than it should be. I already have ideas about improving this for next year. Anyway, I asked this student to draw the curve on the board and nudged her in the direction I wanted. I probably gave away my thoughts and she probably shared this idea with a bunch of other students. That’s alright, they’ll earn points and they have a seed planted that might come to bloom. However, a few students presented an argument I did not anticipate at all. A GeoGebra sketch will help:

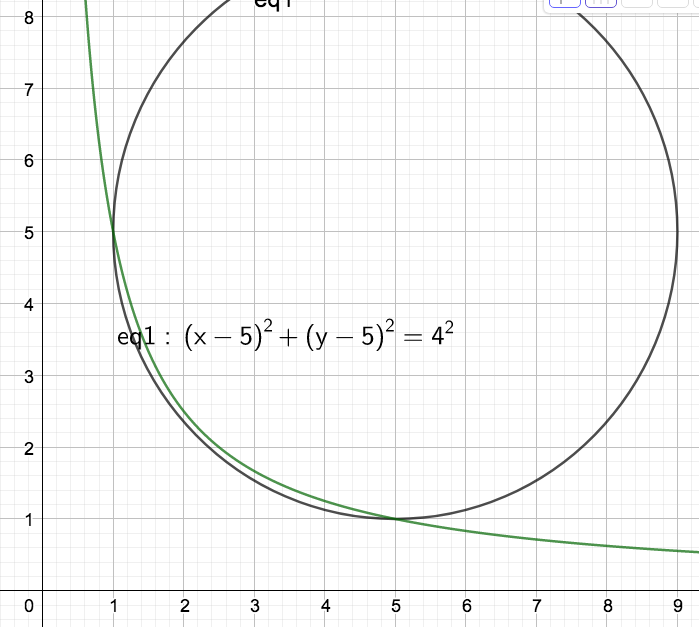
A few students observed that the arc in question seems pretty similar in length to one quarter of the circumference of the circle in the diagram. They concluded that 2*pi would be a decent approximation. Calculus tells me that 6.1448 is the length. This a fantastic approximation and it is pretty fantastic thinking. These students knew that they did not have a formula for the length of the arc along f(x) = 5/x but they do know how to find the length of an arc on a circle. I am pretty proud of this line of thinking and I want to brag about them here tonight and in class tomorrow.

Thinking About Stories

One of the newer initiatives at our school is to help students listen and tell stories. We partnered with an organization called Narrative 4 (you can see their work here) I am simplifying the mission here a bit but the idea of storytelling is on my mind for a number of reasons. Next Wednesday our sophomore and freshmen students will participate in a Narrative 4 workshop sharing songs that mean something to them and explaining why. I love the power of stories and am prone to share them myself to try to make a point. I was reminded of this in the Empowered Problem Solving (#epsworkshop) run by Robert Kaplinsky. He made reference in one of the videos in a study module to ‘the story we are telling in our math class’ and this made me think of a recent frustration with our precalculus book. It all comes together, at least in my mind! Anyway, we are starting our unit on conics and our text, as many do, suddenly changes format of how a parabola equation is presented. Our students are used to y – k = a(x – h)^2 and this format makes sense to them. We can easily adapt this to x – h = a(y – k)^2. Suddenly, we are talking about the directed distance from the vertex to the focus and we introduce this new constant p. Okay so far, right? But suddenly, my students see 4p(y – k) = (x – h)^2 and they see 4p(x – h) = (y – k)^2. Why? It is pretty simple to let them know that the a that they have grown to interpret has a side personality as 1/(4p) It is easy to find a point on the curve and show distances that are equal to each other. I do not want to ignore the examples in the text because my students use it as a reference and a resource. I also do not want to stray from a meaningful way to write equations simply because of the whims of our textbook author. I also suspect that so much of what kids learn in school feels like an arbitrary set of equations and definitions and I want to battle that. I want the story in our math class to be that this is a journey together that builds on what we’ve known before. A journey that ties ideas together. A journey that feels logically coherent and consistent to the best degree that I can possibly make it. Lofty goals, I know. I just find the weird changes like the one above undercut that sense of logic, consistency, and damage the connective tissue of ideas that I try to nurture. I am almost certainly overreacting to this weird quirk of Precalc texts, but that feeling was amplified when I thought about our storytelling exercise at school and tried to reflect on Robert Kaplinsky’s message in our workshop. I love it (LOVE IT) when my brain is agitated by these ideas, when I see connections and themes in my life. I try to share that joy (agitation sometimes!) with my friends, colleagues, students, and you, my dear readers.