Month: August 2018

About three years ago I made a commitment to myself. I was still living with my family in one of the boys’ dorms on our campus and was living within a pretty strict clock regimen of dinners at the dining hall, study hall hours, lights out (ha!), and rotating dorm duties. I made a decision that I would close my computer when I left my classroom at 3:30 and not open it again until study hours started in the dorm at 8 PM. I managed to maintain that commitment (mostly) for the year. I was regularly up later than I really wanted to be due to dorm duties and noise. I was up early every morning catching up on work, but I had every afternoon free of staring at my computer. I hung out with my kiddos, we played on the dorm lawn, we ran around with friends on campus, I sat at the dining hall and caught up with folks. Part of what made it possible to carry out this goal was that I was teaching four classes that year, most years I have taught five.

This year I am teaching four classes again and, once again I made this commitment to myself. This past week was our last week before classes. I took the time to take each of my children to see movies. On Thursday I took my son to see the new Spike Lee film. It was terrific. On Sunday I took my daughter to see Christopher Robin. It was sweet and tender. A bit predictable, but filled with good nuggets. I got emotional on a number of occasions because I have become that dad. But I walked away renewed in my sense that I need to create space. I need to put that laptop away for awhile. Email will be answered eventually. My job as a teacher and a department chair is not THAT important that a few hours will get in the way of carrying out my responsibilities in a meaningful, humane, and productive way. I can just be dad and husband for a few hours. I can hang out on the hammock. I can sit and chat about music with my boy. I can watch my girl play with LoL dolls and her Baby Alive crew. I can sit on the porch and read. I can listen to some music and just be. If I do this the right way, then when I open my email and my files I will probably be a better colleague and a better teacher.

Sometimes ‘Doing nothing leads to the very best something’ as a silly old bear once said.

 

Some writing about teaching again soon. But it won’t be done between the hours of 3:30 and 7:30 PM!

I am not 100% sold on how I have divided the data, but I want to think out loud about how my opening day activity for Precalculus Honors is developing.

Last year, I took the advice of a number of online colleagues and divided my classroom into table sets of 3 for student groups. I anticipate that I will have five of these student groups in Precalculus Honors (PCH from now on in the post) so I set up five subdivisions of the data that I previously shared (in this post) and I will start off with the cleanest of the data sets. At the bottom of the post I will attach GeoGebra file links as well as the current status of my handout. I will present screen shots of the data subsets and discuss my hopes and dreams for how this activity will unfold.

Group #1 will have an image similar to this when they graph their data. I will share this exact one with the whole class. I set up five GeoGebra files with the same screen dimensions (at least I think the dimensions are exactly the same, hope so!) My hope is that this will feel largely quadratic to them. I do not think that they have previous experience with regression equations on their TI or with any online tool. I am suggesting that they use Desmos in class. I will present GeoGebra with the goals of exposing them right away to two of my favorite tools. We’ll discuss which one might feel better for different situations. In the past few years I have had a number of students adopt both programs as a natural part of their problem solving. On more than one occasion a student has written a note on a problem set along the lines of ‘Desmos agrees with my conclusion!’ A natural direction for them to go is to use point H as a vertex and develop a quadratic that fits this reasonably well. Hopefully, we can incorporate a discussion throughout the year of the messiness of real world data compared to mathematical models. I love quoting George Box here – ‘All models are wrong, but some are useful’

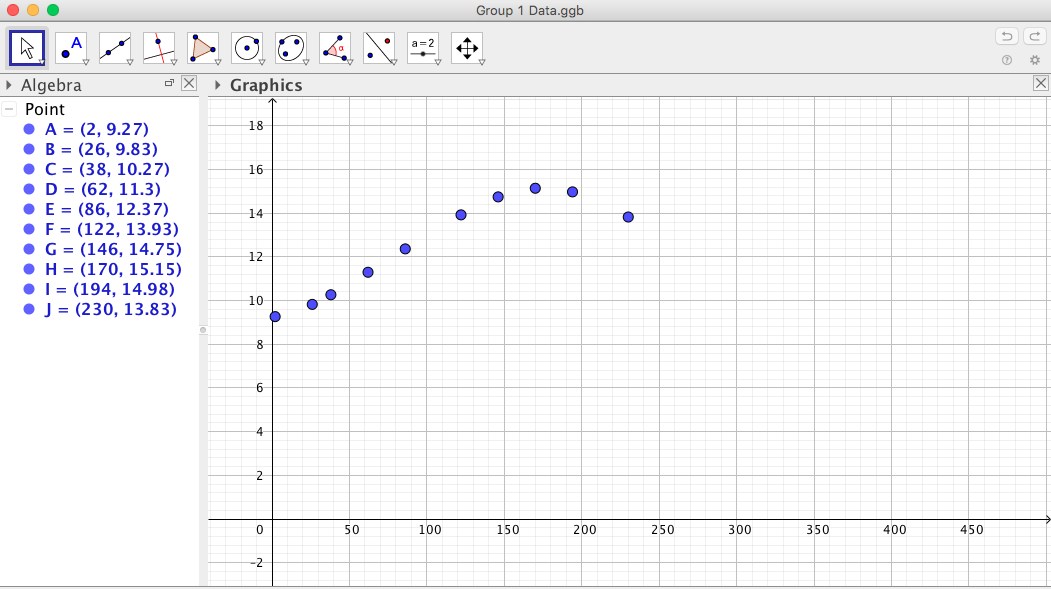
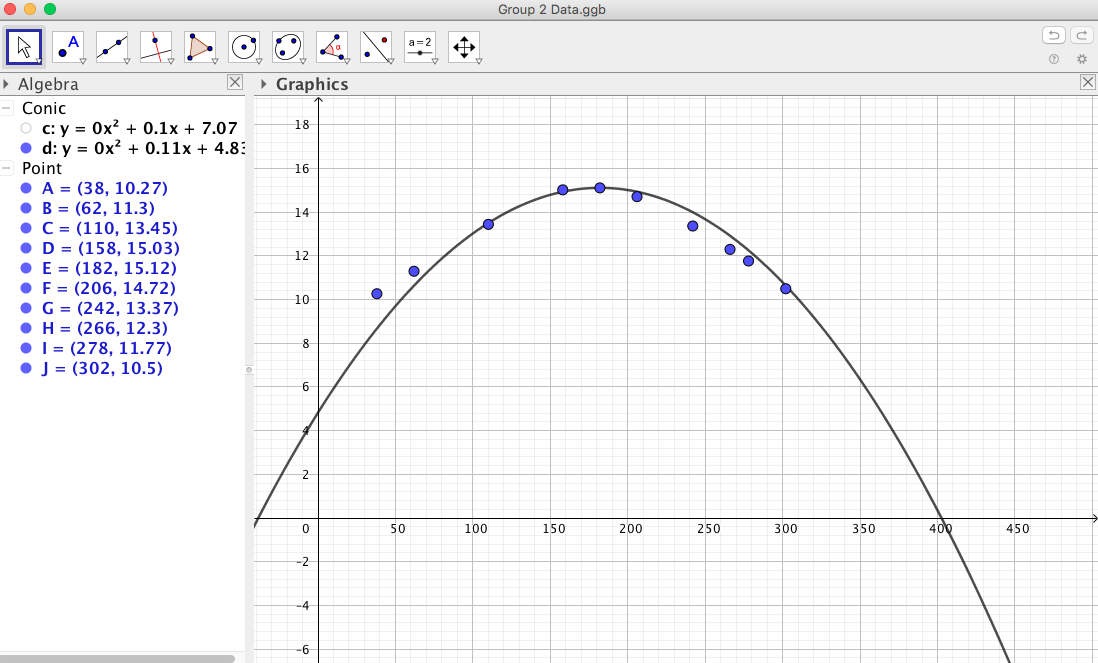
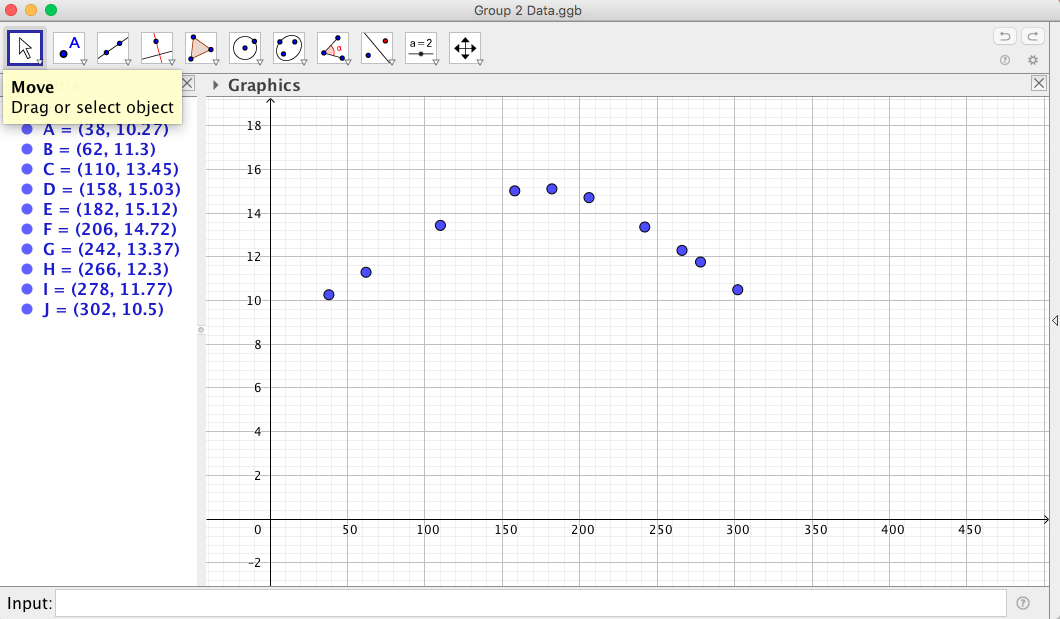Group two will generate something similar to this image. Again, I am anticipating a quadratic guess. This time point E should be seen as the vertex. Playing a bit with my TI and anchoring my guess at point E yields the following promising picture. 

Now, we are getting somewhere!

Group three sees this data and has some decisions to make. This is where I am really questioning myself. I worry that there is too much here for a first day activity. I think I may tweak this data set so that it is also more deceptively quadratic in nature.

Group 4 picture above.

Group five data picture.

And, finally, the whole set together here –

As I write this and think about my goals for that first day, I am sure that I want to modify the data that group 3 gets. I don’t want this play to become frustrating on day one. Let’s save frustration for later on!

I am hoping to plant seeds for a number of interesting conversations to have over the course of the year. I want the students to think about decisions based on small sets of data versus larger sets. I want them to think about periodicity and where/when/why to expect that behavior. I want to present them with an intentionally open question on our first day together to set a tone for open questions together throughout the year. I want them to remember something fundamental about quadratics and I expect to present two forms (standard and vertex) on the board after a little nudging from the groups.

I worry, as I often do, that I am being too ambitious. We have about 30 minutes together on day one due to a whole school convocation that day. I am really debating whether to make this the activity and conversation for our first full class day together. In that case, I would pull out an old favorite problem to have as the conversation seed for day one and mix in a bit of the boring old syllabus, etc on day one. Any advice there?

Here is a link to a dropbox folder with the GeoGebra files as they currently are arranged as well as my Word handout.

As always, advice/comments/questions are welcome here or over on twitter where I am @mrdardy