Our school has a two week spring break that happens at a time in the year that does not feel much like spring in our part of the world. My Precalculus Honors class is due to start a chapter on systems and we will learn to work with matrices. However, for the intro to the chapter I knew I wanted to revisit old skills in a new, hopefully more interesting, way. I had the germ of an idea last Thursday (IIRC) and I sent out a tweet to my math team.

I thought that this would be a fun sort of open way to get my students thinking again about systems. As the #MTBOS is inclined to do, I immediately got helpful feedback. Among the suggestions were to make sure that the line was not horizontal or vertical as this would be WAY too easy. Noted! Nice suggestion.
A favorite early suggestion came from a teacher I had not interacted with before on twitter (at least I do not remember any extended interaction)
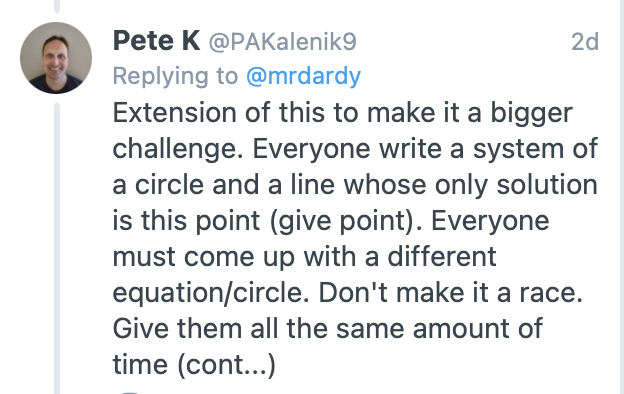
This got my mind working at a much deeper level. I had kind of thought of just throwing out a quick challenge question. This suggestion, and the resulting conversation, got me thinking along the lines of a more organized activity leading to this challenge question. A few more exchanges with Pete and with a couple of other twitter pals and I landed here with a great suggestion from Karen.
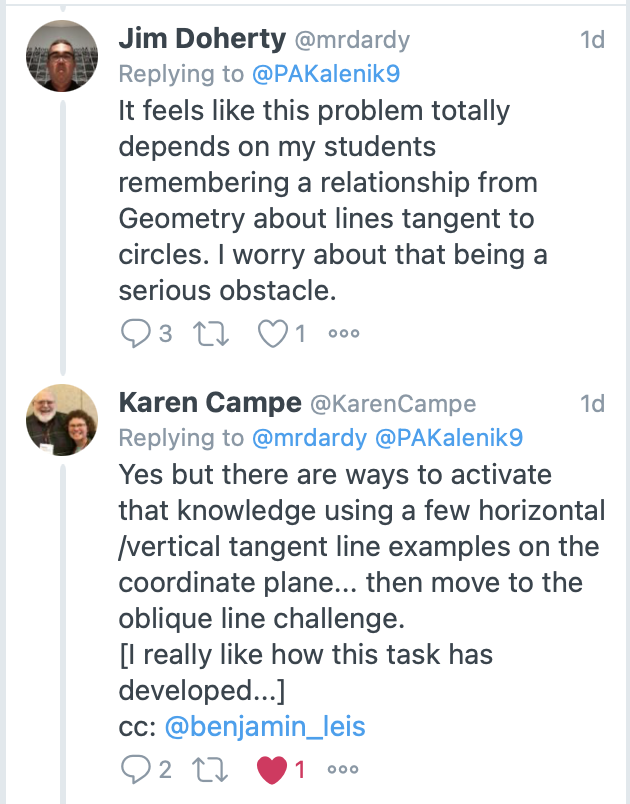
After a few more tweets back and forth, and with school looming finally, I crafted an activity (you can find the finalized product here )and shared this link out to three twitter pals who were pretty actively engaged in this conversation. I was so touched by the fact that all three of the folks I shared the doc with took the time to look it over and share some ideas/questions/insights into how I constructed this. Years ago when I first started blogging then took the leap into twitter this kind of collaboration and sharing of ideas was exactly why I took that leap. I feel remarkably fortunate to have found this community of open, curious, and generous minds.
I decided to jump right in on day one back and present this activity to my small Precalculus Honors class. I have seven students in this class and they normally work in two small groups. One group of three boys usually work together and another group of four students (two boys and two girls) usually share their ideas together. I specifically asked them to start this work on their own and I spent the first ten minutes or so of class just sitting quietly and trying to spy on the work that they were doing. I have small whiteboards at our big Harkness-style table and most students do their thinking on those whiteboards rather than in a notebook. After a little while I began taking notes on our GoodNotes app and asked the students question by question to share their ideas. You can find our class notes on the hyperlink in the previous sentence.

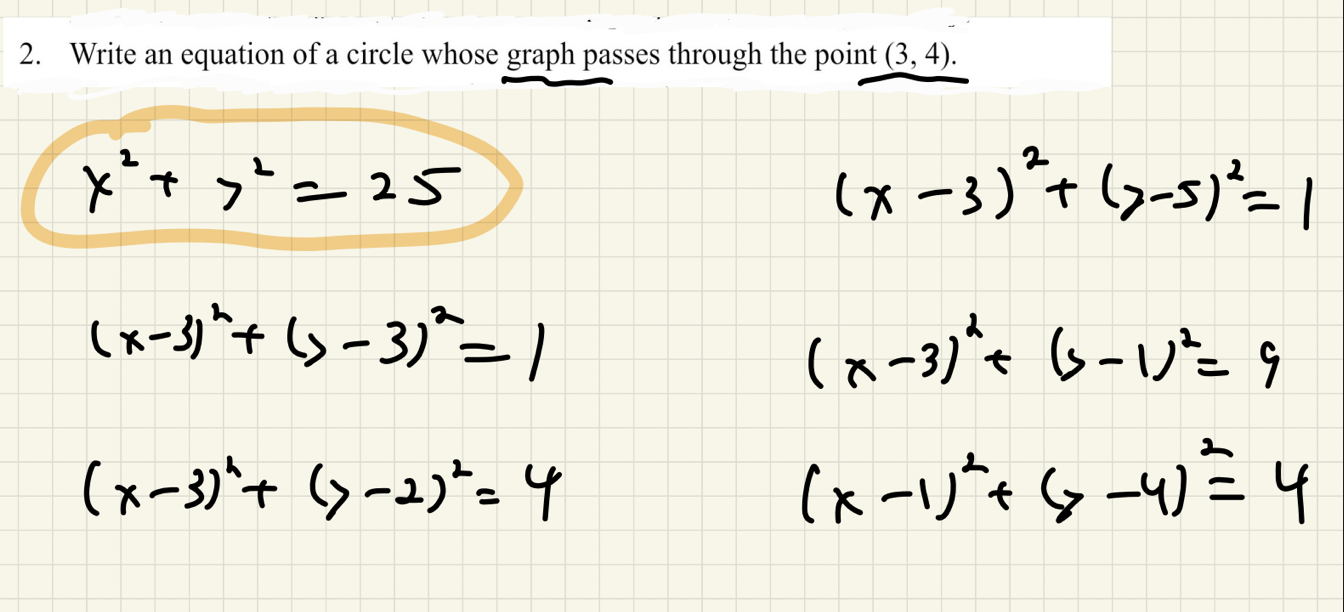
Next, I asked them to sketch their graphs and identify how many intersections there were. They were asked to find the coordinates of the solutions to their system. I suspect that few of them recognized right away that the point (3, 4) had to be one of their solutions, but that is fine. Not too much time or energy was wasted here. Now comes the payoff for the activity.

As soon as Ava shared that she remembered that a circle and a line that intersect once has this special name from Geometry (with a little prompting from me) her neighbor Abby immediately remembered the perpendicular slope notion. Once Abby said this out loud a couple of her classmates nodded in recognition that they, too, knew this at some point. Now we were off to the races. The link I shared above to the GoodNotes file has a number fo Geogebra sketches for the circles and lines that my students developed. We had a great conversation about whether it was easier to think first of the circle or the line first (we seemed to agree that the line as a starting point was more efficient) and everyone was pretty engaged in the conversation. I am pretty thrilled about how well this went and how my students were able to dissect this in our 45 minute class today. I want to thank Pete K (@PAKalenik9), Karen Campe (@KArenCampe), and Benjamin Leis (@benjamin_leis) for their thoughts and this activity was so much richer because of their contributions.