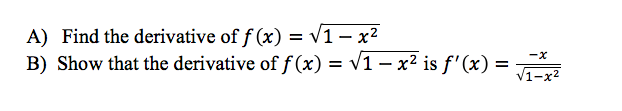This post is inspired by a twitter exchange with the awesome Joe Schwartz (@JSchwartz10a) and by a running exchange with one of my Geometry students. Joe tweeted out the following picture: 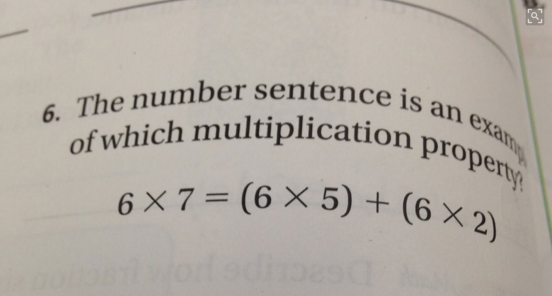
The picture was accompanied by the question : “Do 3rd graders know the answer to this question? Truly curious.” It just so happens that my Lil Dardy is in 3rd grade. I showed her the question and (briefly) explained the equation written. I replied to Joe that she was not surprised to see it written that seven sixes is the same a five sixes plus two more. However, she did not know any vocabulary word to describe this. Joe replied, succinctly, “And she doesn’t need one…” It made me smile. It also made me think when I was reviewing for a test with one of my Geometry classes. We just finished a chapter on triangle bisectors and centers. Loads of vocab in this chapter. Very few new skills, just new words describing relationships. Thinking back to the exchange with Joe I found myself questioning my decisions in writing the book and in teaching this chapter. During the test review a student asked if there would be any vocabulary on the test. This particular student has asked this question before just about every test. I answered the way I do just about every time. I told him that he needed to know what these words mean to accurately interpret the questions at hand. For example, if I ask about altitudes to a triangle, he needs to know what that means. However, there would not be a question where I simply ask him to replicate the definition of an altitude. Thinking back on this exchange, and this way that I answer the question, I have a ton of questions that I need to ask myself and I will start by posing some of them my readers out there.
- My guess (an uncharitable one) is that the student asking about vocabulary is looking to avoid committing anything formal to his short term memory before a test. Admirable in a certain way, but what does this question say about what he thinks his job on a test is? Why would students who have been working with words day after day express any serious concern about being asked what those words mean?
- Real people have real vocabulary that they use in their studies, in their work environment, etc. I recoil at the suggestion that I should do something objectionable now because someone will do it to my students later. But, I am beginning to wonder whether I am cheating my students a bit. Should I be more emphatic in urging them to be careful about vocabulary now so that they will better understand what they read or hear later? Am I being lazy when I let them casually refer to the longest side of any triangle as the hypotenuse? [Note: I have written about this before. I DO correct them, but in a pretty gentle, nudging way. I remind them every time that the hypotenuse is a specific name, but this habit has settled in with my students for a couple of years now.]
- What are we communicating to our math students if we mark points off or hold them accountable in some ways to formal language if they can get their mathematical ideas across through their work? Are these skills dependent upon one another? Is it okay that my students can swing into action and write the equation of an altitude of a triangle but be uncomfortable and vague if asked to write a definition for what an altitude of a triangle is? As someone who is so comfortable with these words, I struggle to understand how someone can write that line without being comfortable that they can write a definition, but I’ve been teaching long enough to know that this is a real thing.
- Is this another instance where students have been trained to think that there is one right way to answer a question and their job is to make sure that they simply regurgitate (if they can decode correctly) what that correct answer is. I, of course, hope that my grading policies and the way that I communicate in class convinces my students that this is not the way life is in my classroom. However, I know that I am battling impressions that have formed over years.
- More importantly – Does it matter that my students know things like the altitudes of a triangle intersect at the orthocenter? Is there ANY chance that they will remember this in a few months? In the past few years I taught the course, I pretty much only mentioned the word centroid and avoided talking about incenters, circumcenters, and orthocenters. I am not at all sure that I made the right decision then or that I made the right decision this year in explicitly defining them. In my text the words centroid and incenter are explicitly defined. Circumcenter and orthocenter do not even appear in the text. A mistake then? A mistake now? I’d love to hear some advice/opinions.
Gotta get dressed for school now. More thoughts swirling and I hope I am disciplined enough to get them down soon.
Thanks to Joe for prompting this post!
As always, you can reach me here in the comments section or over on twitter where I am @mrdardy