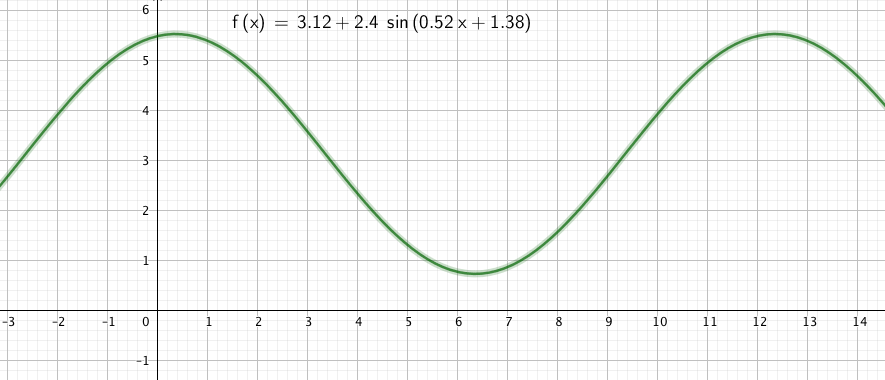
At TMC16 one of the impressive experiences was listening to the keynote speech by Tracy Zager (you can find it here ) and I remember briefly mentioning it in a post soon after the conference. Sadly, I never went back and really dissected my positive feelings about it, but I do know that one of the habits I developed after her speech was to communicate pretty regularly with our elementary school teachers more regularly when I ran across interesting math tidbits. I also know that Tracy has written a well regarded book called Becoming the Math Teacher You Wish You’d Had. I have not read this book (yet!) but the title of the book has been haunting me. I am not speaking with any deep knowledge about the strategies that she is advocating and I may be doing her a disservice, for which I apologize in advance. But as I am sitting here at the beginning of my spring break, I am thinking about what has gone right and what has gone wrong so far, 2/3 of the way through my 2018 – 2019 academic year. I also think about the phrase from Dan Meyer’s TED talk, ‘Be Less Helpful’ and this morning I want to try and wrestle with each of these phrases that are resonating in my head.
I will admit up front that my interpretations of these two phrases are my interpretations. I also need to fill in a little background to explain how I understand Prof. Zager’s phrase. I had two high school teachers who were enormous influences on me. I had the same English teacher, Mrs. Myra Schwerdt, for my junior and senior year. The way her typical class went was this – we came into class, she tossed out a question prompted by our reading assignment from the night before and then she moderated the discussion. Tossing out another question if the conversation ran dry or probing someone on an opinion/interpretation that they made. She was sort of first among equals in these conversations. I never felt that she forced us to interpret anything in any way but I also felt that we better have some backing for what we had to say. In my senior year I took AP Calculus BC from Mr. Barry Felps. A typical day in that class started off with a quick look at a new idea with Mr. Felps offering an example or two of ‘how to’ after explaining some new idea. He would sometimes go over a HW question or two from the recent past (often after his go to joke, we’d ask ‘Mr. Felps, can you do problem #12?’ He’d look at the book and nod while saying ‘Yep’. Still cracks me up a bit thinking about this…) After this, typically 15 – 20 minutes total, he’d say ‘Okay, you have work to do and so do I’ He would sit and we would work with our neighbors and friends. If we got stuck, we’d go ask him but most of the time we felt that we wanted to figure it out ourselves. We also had a study group that would periodically meet on Sundays for a combination of football, pizza, calculus, and physics. So, here I have in my mind what ‘Be Less Helpful’ looks like (to my 17 year old self for sure) and an image of the math teacher I wish I’d had (which, I feel enormously fortunate to say is a math teacher I did have)
Fast forward from 1981 – 1982 academic year to the 2018 – 2019 academic year. This year I am teaching four different classes with pretty different groups of students. I teach Geometry with the text I wrote four years ago to mostly 9th and 10th graders, I teach a Discrete Math elective to mostly seniors, I teach a non-AP Calculus class to a mix of juniors and seniors, and I teach AP Calculus BC to a mix of juniors and seniors (with one brilliant sophomore in the mix) These classes all have different needs and different inherent investments from the students involved.
It is, of course, unfair to generalize too broadly, but I think it is fair to say that the general needs/wants of these classes differ. I try to account for that, but I know that there are some tendencies in my teaching that appear in all four subjects. I ask more than I tell. I redirect questions to other students to get their input. I have student in groups of three facing each other. I randomize these groups so that a group of three is together at most for five classes. I write problem sets that dip into past knowledge and ask some questions for which we have not been explicitly prepared. My quizzes are narrowly focused on recent information and they are weighted less than tests. My tests are all cumulative in nature but they are about 70% focused on what has happened since the last test. I want at least one test question to feel novel, to ask students to put together information in a way that feels new – a problem rather than an exercise, I guess I’d say. We have a test correction policy that we adopted this year (you can read about that here, here, and here ) and this policy seems to have helped reduce anxiety a good bit. All of this is to provide a little context into my classroom and my vision of what these phrases ‘Be Less Helpful’ and ‘Becoming the Math teacher You Wish You’d Had’ mean.
What I have struggled with, this year more than in the recent past, is the discrepancy between the math teacher I wish I’d had and the math teacher that my current students wish they had. A good number of my students seem to be happy wth how our classes run. I have posted a number of entries this year about student success. I have received some lovely emails from parents of students in Geometry, some nice remarks passed along from colleagues about students in Calculus Honors, some terrific conversations with students in Discrete Math, and an abundance of energy and creativity from my AP Calculus BC gang. In all four of my classes I feel I am reaching some students and making a positive impact. What concerns me, and what prompts this post, is the fact that a number of students are not buying what I am selling. They are frustrated when I respond to a question with a question. They think it is unfair to have a test question that does not look like something they have explicitly practiced. They feel that I am off loading my responsibility as the teacher when I ask them to work in groups to figure something out instead of lecturing and telling them how to figure it out. I have students across a wide range of abilities and a wide range of reactions to what I am trying to accomplish. It is important that I recognize this and do not simply bask in the glow of the students for whom this approach really clicks. Where I struggle, is trying to reconcile what I think I understand about teaching research, what I understand about NCTM’s recommendations, and what I valued as a student with the discomfort and unhappiness that I see in some of my students. I also struggle with balancing what is clearly working with some students in each subject. I don’t want to lose that energy and motivation that I see in students who value what feels like a different way to experience math. I know that this is not an either/or situation. I have two weeks of spring break to think and reflect. I know that there is a way to reach the frustrated kids without giving up the the facets of my class that are valuable to some of their colleagues (and to me!), I know that there is a balance to be struck between asking kids to step out and feel challenged and making sure that they still feel supported.
I think back to a comment from a student abut 6 years ago. About three weeks into the school year she asked for a personal conference to talk about her struggle in our Honors Calculus class. By the way, struggle for her meant that she had a B average instead of her typical A. She said to me ‘I thought that I needed to learn formulas and how to use them. That isn’t working here.’ She and I had a lovely conversation and in the years since I have run into her dad a number of times. He always tells me how important my class was for his daughter. She has sent me lovely thank you notes updating me on her progress. She is an example of a student I was able to help cross a certain threshold. I want that feeling for all of my students in some way or another and I have solid evidence that this is not happening often enough right now. I have some serious thinking to do.