A super quick post this morning. On my last problem set for AP Calculus BC I included the problem below:
A 10 m rope is fastened to one of the outside corners of a house, which has the form of a rectangle, 6 m long and 4 m wide. A dog is fastened to the rope. What is the perimeter of the region that the dog can access?
I have asked a form of this question a couple of times over the years. One year I did not mention that the rope was on the exterior of the house and I had a student assume that the dog was tied to a leash inside the house. I fixed that mistake.
A GeoGebra sketch below shows the image I have in my head for this problem. 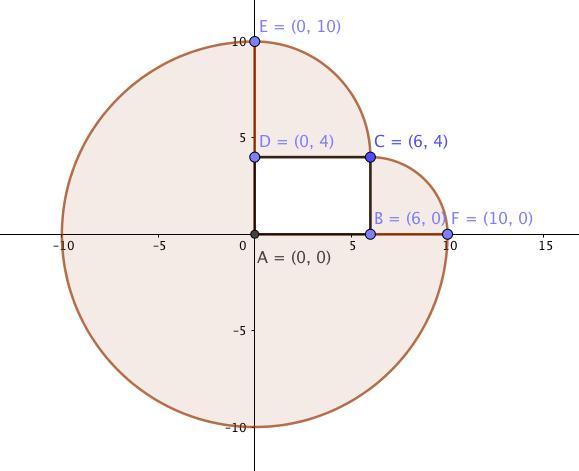
My answer to this question, and the answer that 11 of my 14 students had, was that the perimeter is 20π. Two students argued that the answer should be 20π + 20. Their argument is that the borders of the house, the sides of the rectangle in the drawing, are also part of the perimeter. I loved the debate that ensued and most students migrated to this point of view. I reflexively thought of perimeter as exterior, while these two students argued that perimeter is boundary. I think I agree with them and I LOVE the fact that they cared enough to debate this on a problem that counted for one point out of about 400 something for the term. I also LOVE that students who got their answer marked correct started arguing against the answer that they arrived at.
Followup – Where should I place the rope to minimize the area I have to check for poop? To maximize the area the dog can roam?
Definitely using this one!
You got me curious, so I made a desmos graph to play with:
https://www.desmos.com/calculator/rn4e6kplgl