We have adopted a new schedule at our school and we are on a seven day rotation this year. At the beginning of each rotation, I give my AP Calculus BC students a problem set that is due at the beginning of the next rotation. These are just grab bags of problems that I find interesting. Some are calculus problems, but most are just fun stuff I have gathered over the years. On our most recent problem set (the last one of the year) I gave a problem that I think I found in an Exeter problem set. The heart of the problem was the image below. 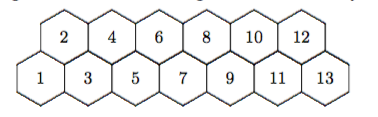
We are told that we are to start at hexagon #1. We are allowed to progress at each step to an adjacent hexagon as long as that hexagon has a number higher than the number we are currently on. So, for example, from 5 you can proceed to 6 or 7 but cannot go back to 3 or 4. The question is to determine how many pathways are possible from hexagon #1 to hexagon #13.
I did not know the answer to this question, but I was confident that I (and my AP Calculus BC students) could find the answer. I approached this problem the way I do many problems, I wished it was smaller and I hoped to see a pattern emerge. I have advocated this problem solving strategy with my students but few pick up on this. I think that this has to do with their sense of freedom as mathematicians. I think that changing the problem feels like a privilege that they don’t think that they have. Need to work on this…
So, I built up a table and saw that if there was just one hexagon then there is just one path. A boring one of standing there. If there are two hexagons, there is also only one path. Hmmm, not promising yet. Three hexagons? Two paths, from 1 to 3 or from 1 to 2 to 3. Four hexagons? 1 to 2 to 3 to 4, 1 to 2 to 4, and 1 to 3 to 4. Now, I am confident that Fibonacci is hiding here. A quick check confirms this and I was pleased with myself for finding a fun problem that did not have an obvious solution.
I used the word obvious for an in-joke. One of my particularly clever AP Calc students will routinely refer to things being obvious in class discussions. His name is Owen and the way he marked his diagram was interesting to me on his problem set so I asked him to explain this in class. He started essentially the way I did but instead of a chart he simply wrote a 1 in the 1 box for # of paths and a 1 in the 2 box for the same reason. Now, his explanation gets interesting. Next, he mentions that it is obvious that if you get to hexagon 3 you have to have gone through either #1 or #2 so that the total number of ways to get to #3 is the sum of these two other numbers. Similarly, to get to #4 you have gone through #2 (one path) or #3 (two paths) and now Fibonacci is obvious. I was so delighted by his approach to this problem.
So I decided to present this problem to my other classes to see how they might approach it. In each class I explained my result after allowing them about 8 – 10 minutes to share thoughts about the problem with their small group partners. While none of my other students arrived at a conclusion in this relatively short amount of time, they did have some interesting approaches. One of my Discrete Math students tried to leverage what he’s learned about combinations by starting with the notion that a pathway along the odd numbers is six steps. Then he said that we could add one even number and this could be done one of six ways. We could add two even numbers to our path. This could be done in 15 ways (using combinations or Pascal’s triangle) and he wanted to simply add all of these up. A super cool idea but we started to see problems here. For example, if we add 6 and 8 as stops along the way in a row, then we have to skip hex #7 so we started trying to enumerate all of the path restrictions. Similarly, we realized that we’d need to individualize the number of odd hex visits in a similar way. Daunting, but a great example of trying to use knowledge he has gained this year. A group in Geometry recognized that the shortest path had six steps and the longest had twelve. They wanted to enumerate the number of pathways broken into these categories. A great idea and a way to get a handle on smaller cases to imagine. They quickly became frustrated by the daunting task of keeping track of these tracks, but I loved the idea.
It was a fun couple of days batting around these ideas. I have been really thinking about the distinction between ‘problems’ and ‘exercises’ and problems like this one reinforce the ideas I am wrestling with. I am determined in each of my classes next year to have homework and classwork assignments labeled as ‘problem sets’ or as ‘exercise sets’ and I am hoping to help develop some clear strategies with my students to use when they encounter a genuine problem in math.