So, the session I wrote about a few days ago (you can find that post here ) continues to pay dividends. Yesterday my Precalc Honors kiddos had a test. Today we were to begin discussing vectors. I had what felt like a pretty clever idea this morning. I started off by posting this image (stolen from the opening evening problem that Amy and Allyson shared with us )

I got a quick question back asking if the dots were equidistant. I confirmed and then my students began to quietly count. I encouraged them – as I always do – to chat with each other and I was hearing things about medium sized squares, big squares, etc. I suggested that some more formal classification might be helpful. A couple of kids quickly concluded that there are 30 squares to be formed. This is a correct answer under certain restrictions. unfortunately, these restrictions were not placed on the question. A student named Max said 40 out loud, then said 50. This shook up the crowd a bit and people began to dig in. However, they were hesitant to debate Max because he has a reputation (well deserved) for being pretty on point with questions like this one. SPOILER ALERT: I AM ABOUT TO UNVEIL OUR SOLUTION. IF YOU WOULD LIKE TO AVOID THAT AND THINK ABOUT IT FOR AWHILE FIRST, COME BACK LATER.
Still with me? Good, happy to have you. I went to the board and drew a square of side length sqrt(2) and got two great reactions right away. One person called this a diamond but acknowledged it is also a square. Another said we should redefine squares to avoid this. I then stepped out of the way to encourage discussion about sizes of diamonds that could be formed. We had a list on one side of the diagram listing number and size of ‘squares’ and developed a list on the other side of the number of, and size of, the different diamonds. We had some great debates about the parameters here. We decided that the only diamonds had size lengths of sqrt2, sqrt5, sqrt8, and sqrt10. We were unsatisfied with the seeming lack of a clear pattern here. You will see in the picture below how I tried to impose a little bit of order on the counting by making sure that I identified groups of diamonds or squares in numbered sets that were all perfect square integers in their count. What you will also see in the picture (coming soon, I promise!) is that I pivoted the conversation soon to vectors. My Precalc Honors kiddos took a test yesterday and we are prepared to start a new chapter on vectors. I did not particularly advertise that this was the next topic, but it felt like I could pivot in that direction. Many of the kids in this class took Geometry at our upper school with a text I wrote. In that text, I intentionally introduce some vector language early in the year. When I got to school today, I did not intend to pivot from this diagram straight into talking about vectors, but when we were discussing diamonds of length sqrt5 I realized that it was meaningful to distinguish between a horizontal change of 2 with a vertical change of 1 versus a horizontal change of 1 and a vertical change of 2. Time for the photo now and then a little more explanation.
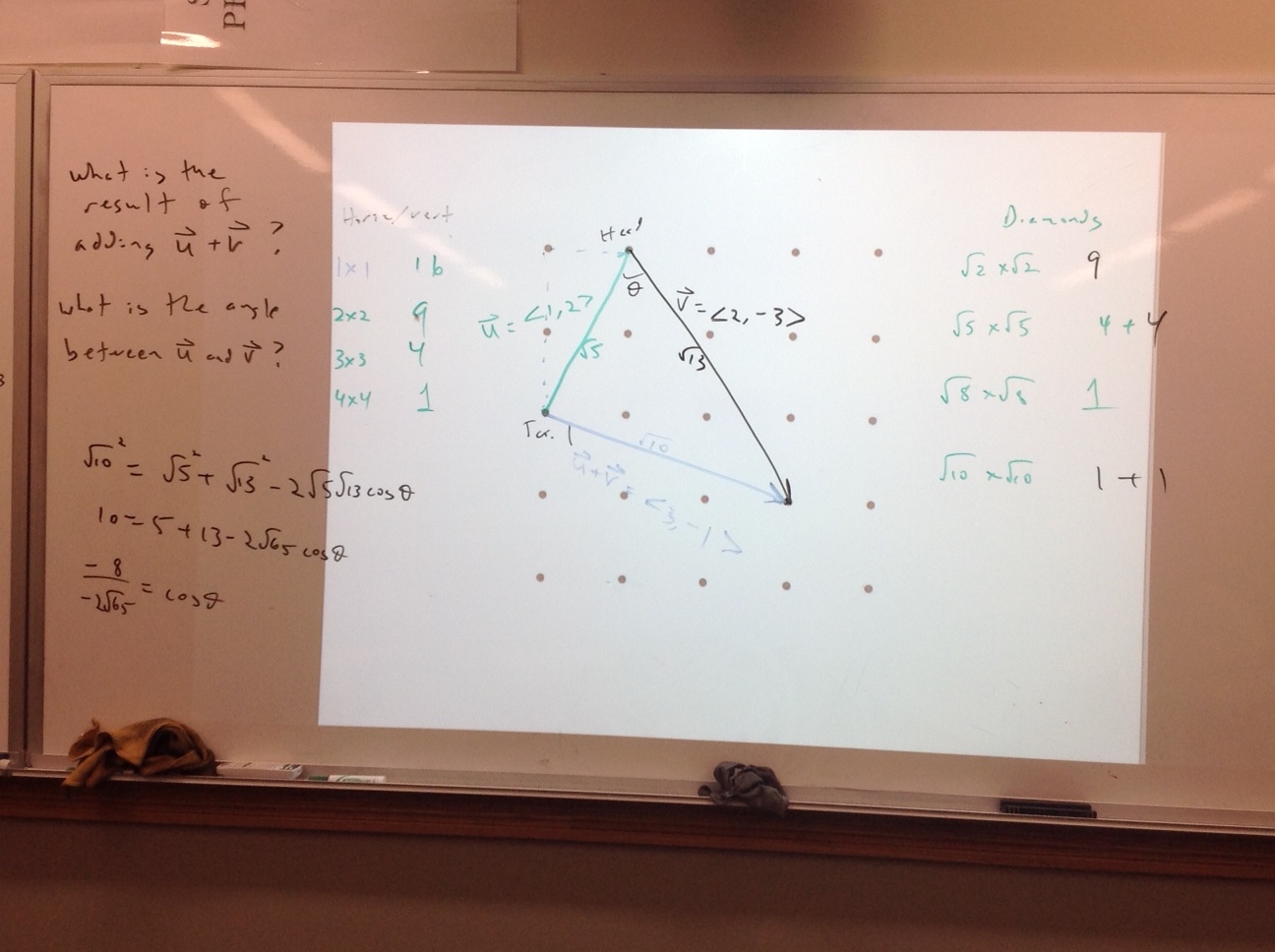
So, in the photo above, a bit of glare there unfortunately, you see a green side of delta x = 1 and delta y = 2. I drew an arrowhead and one student muttered ‘vectors!’ It felt like such a natural trigger and frame to discuss vector notation. Almost instantly kids were discussing magnitude, direction, remembering notation, etc. Man, it was a great way to start the day!
I ended up sharing this problem with a couple of other classes during the day and each time I confessed that my partner and I only found 45 squares and were VERY confident of our answer. Each class figured out where we had gone wrong and they seemed pretty proud that we worked through this all together.
Another opportunity here to thanks Amy and Allyson for the great PD session and I know that I will be pulling some other tricks out of the bag of tools that they provided for us last week.
Hi. This was great fun working on it. Especially when you threw in the diamonds and the hypotenuse (root 2) side. I got to 48 squares. What is the total your kids came up with? Gonna try this with my 8th-graders.
Thanks.
Luis
Many apologies for such a late reply. My gang ended up with 50 as I remember it. I’ll dig around my notes again. How did your kiddos do with the problem?