I have spent the past 25 years teaching at schools that go all the way from kindergarten through high school. I often tell my students that I have a crazy dream that it would be great experience to work with a group of them starting in kindergarten and move up together all the way to high school graduation. We’d REALLY get to know each other and be able to reference ideas/habits/experiences together. I am in no way equipped to teach younger children and I know this is a crazy mental exercise anyway but I do think often about habits and language that my students arrive at my classroom with that I wish they did not have. For example, when faced with the distributive property I always hear what I refer to as ‘that four letter F word’, when faced with a fraction on both sides of the equation I always reflexively hear ‘cross multiply’ [even when there are other factors in a problem] These are just two silly examples of fights that I am too often willing to wage in the classroom. A more interesting one, and one that has deeper implications, popped up in my class last week.
I often have a problem projected on the board when class starts. It is rarely a problem directly linked to the day’s tasks, I just want to get the brains moving and, hopefully, get some conversations started. This year in my Calculus Honors class I have noticed a discomfort with some of the classic word problems of the sort that pop up in Algebra II regularly. This is not a big surprise, these kind of word problems don’t get practiced regularly and there are all sorts of gut feelings that don’t always yield correct solutions. When I throw up a class opener problem I usually make a quick reminder of ‘Hey, look, there is an interesting question on the board!’ On the day I am thinking of, the question I posed was this one:

The first minute or two of each class involves a couple of gentle reminders to attend to the question that is posted and this day was no different. Another minute or so later I heard two remarks almost simultaneously that caught my attention. One student, a boy named Parker, said ‘I know the answer’. He did, by the way, know the answer correctly. Another student, a girl named Maya, said ‘I know how to do this.’ She did, in fact, know how to do the problem but had not arrived at the solution as quickly as Parker did. These remarks instantly caught my attention and I said to the class ‘Did you hear the difference between those two remarks?’ I repeated them both but did not follow down a conversation because I was not sure yet what I really wanted to say. This blog post is an attempt to unpack what I want to say.
I remember back in 8th grade Algebra I having a debate with my teacher Mrs. Hart. I got back a quiz where I lost some credit on a problem despite the fact that I had a correct answer. I asked her about this and she said I did not show her how I got the answer. I offered to show her right then but she told me she wanted to see it when I took the quiz, not at that time. I was pretty unhappy about that, I guess I kind of still might be, but I understand her point. I try to emphasize to my students that I am interested in their thinking in addition to their conclusions. I want to understand how they arrive at certain conclusions. Parker got the right answer to the questions pretty quickly and he briefly explained his logic. I think I understand how he approached it, but I wonder how generalizable his approach was. He is a student with good number sense and quick reactions. He does not always back up his thinking as algebraically as I wish he would. Maya is a more step by step student and is getting noticeably better at explaining her thinking out loud and on paper.
This particular problem is not a deep one but it does remind my students of some system of equations strategies that I know are valuable in their study of Calculus. I also think it is just a good idea to brush off some of those skills every once in a while. Mya had equations written down for this, as did a few other students. Some used three variables. Some expressed the mother’s weight AND the nurse’s weight in terms of the baby therefore only having one variable. I reminded them that matrix operations sometimes help with three by three systems but they (wisely) rejected that memory here. I posted this question on my twitter account (@mrdardy) and had a nice conversations over there with some folks. My favorite conversation was this one:
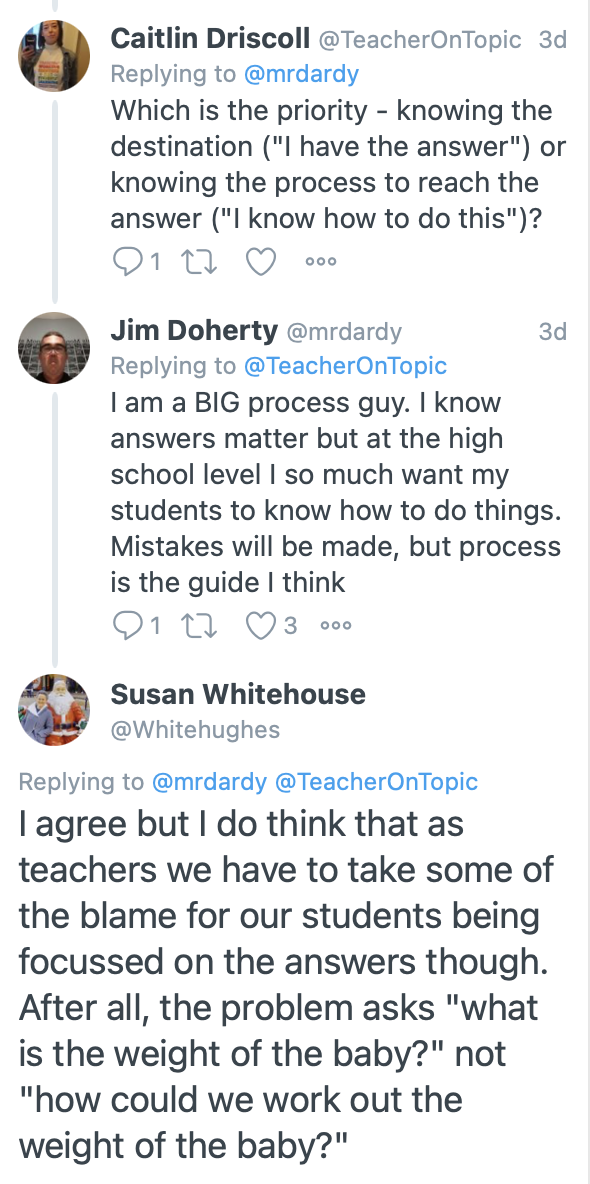
I LOVE the point Susan made here. She is 100% right that the question asked for an answer, not a process. In my defense, and I suspect Susan knows this, by this time of the year we have established pretty well that process and explaining/defending your answer is an important part of what is going on. The question I have, and what I am trying to unpack in my mind, is this one: To what degree is it fair to ask my students to accept the idea that process is at least as important as conclusions? How often in their life is this message actually meaningfully communicated to them? I am sure that they have had teachers, and other adults, routinely tell them about the importance of process but I suspect that they are also routinely awarded for answers. What is the message here? I think that students equate grades with what we value and I understand that instinct. So, if I routinely award full credit for a correct answer without support then I am sending the message that it really is all about the answer. I try to send the message with small point deductions that process matters. What I probably need to do is make more of a commitment to something like a rubric where the actual answer to the question is a small percentage of the question’s point value. This brings other problems with it. I think back to a student in the second school where I taught. She joined our school about a month into the year and she was in my AP Calculus AB class. About two weeks into her tenure at our school she announced ‘You seem to think that AP means All Problems’ She was making a distinction between problems and exercises and she was unhappy about the prevalence of problems on my assessments. I have a working definition, from my Master’s advisor Prof Mary Grace Kantowski. She said when facing an exercise we know what to do right away. We might make a mistake in process but we know what to do. When facing a problem we are not sure right away of the process called for. If I present my students with mostly exercises, then there is not a ton of work to be shown much of the time and I do not learn much about them as learners. If I present my students with mostly problems, then there is process to be presented but some students might not have the time and energy to show me enough of what they know in the time allowed. None of these are new problems for teachers, but they all came flooding into my brain when I heard these two remarks the other day in my class.
I think I want to follow up with that class later this week to try and unpack the conversation and try to probe a little on where they land, and where they want to land, when faced with problems in this class. While the goal, understandably, is often ‘I know the answer’, I hope that there is at least some recognition that ‘I know how to do this’ is a pretty good place to be.