Category: Uncategorized

Well, It’s been a while

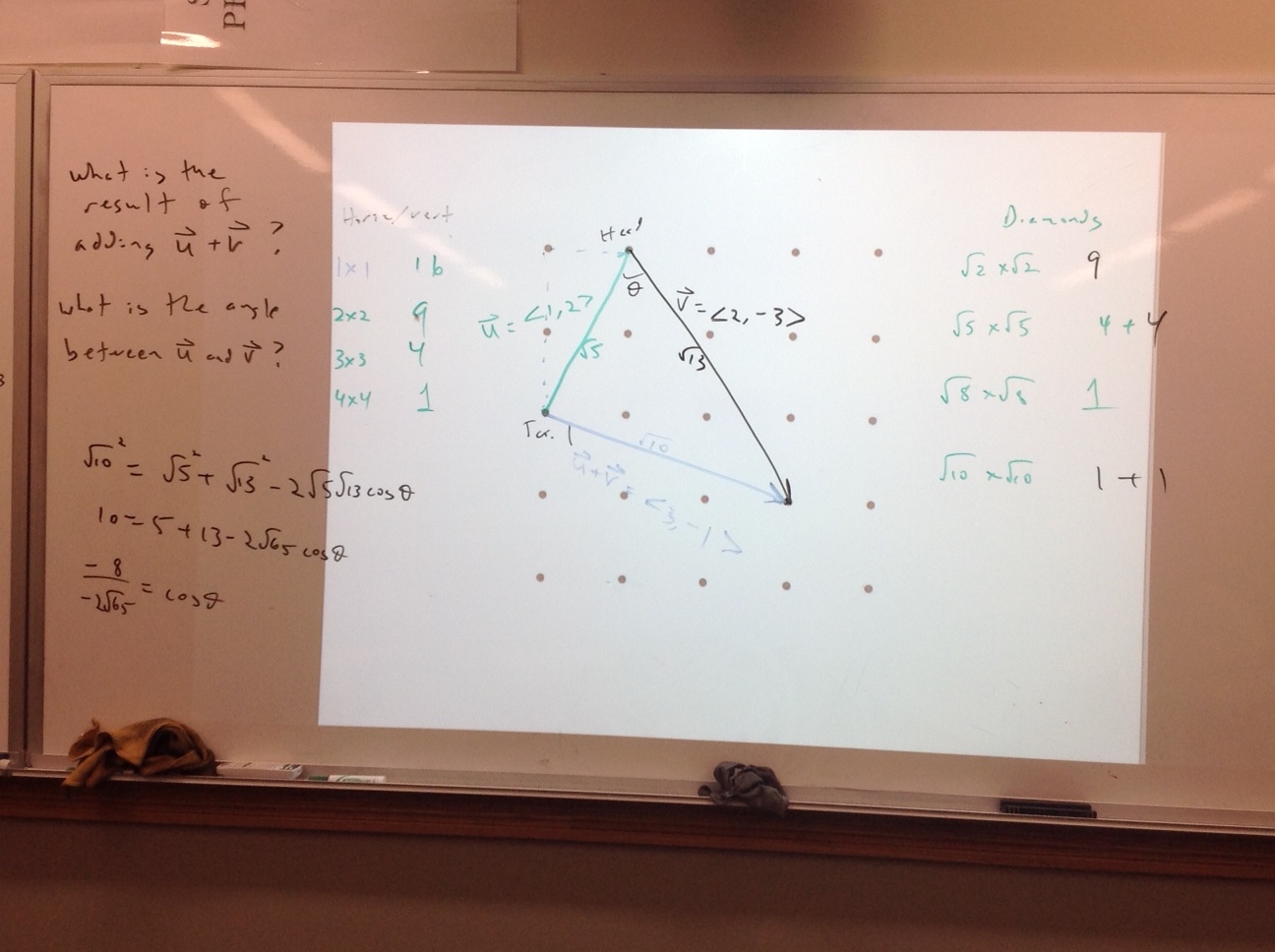
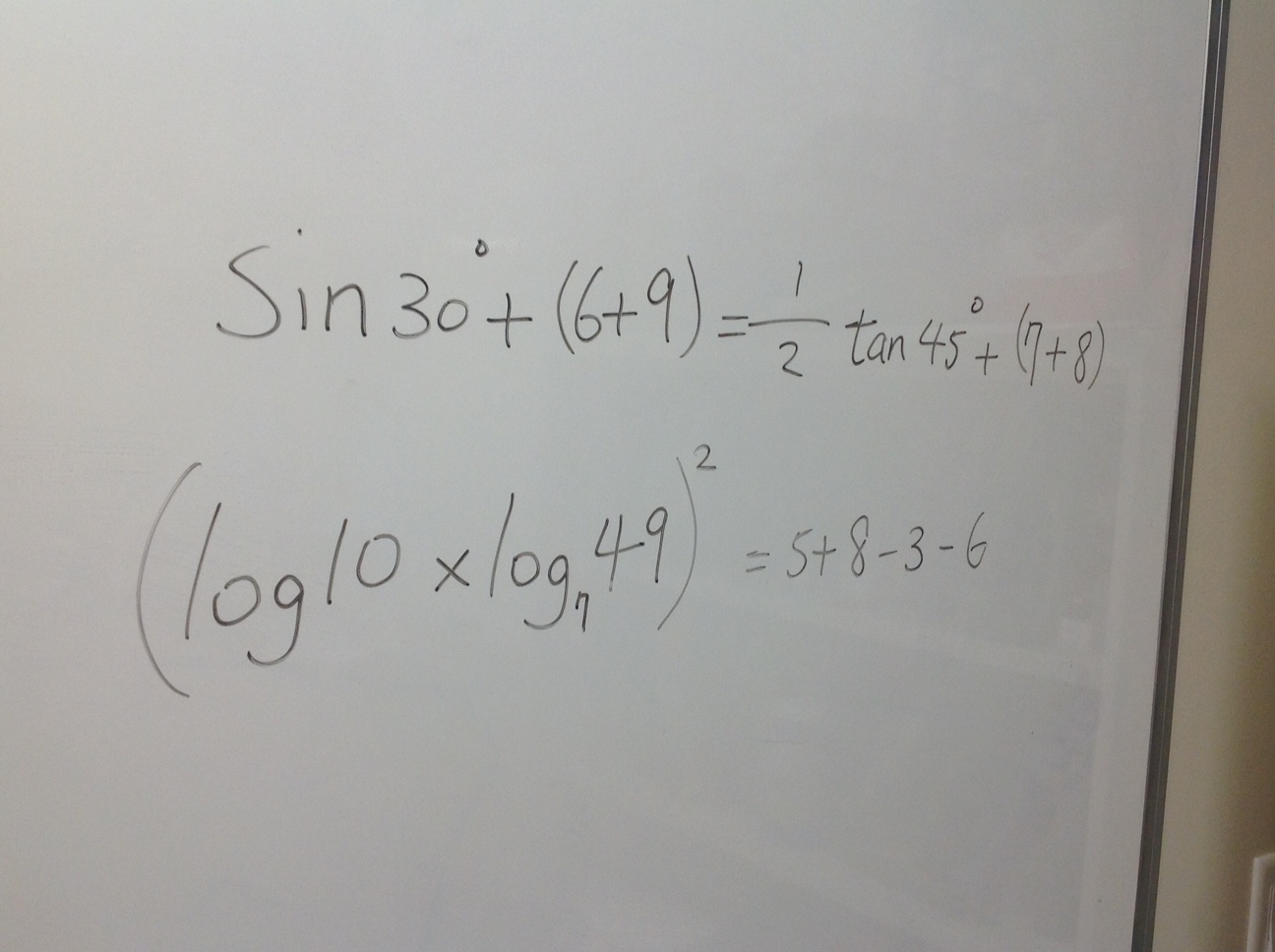I am out of practice at writing here, let’s see how this goes.

My last post was 14 months ago for all sorts of reasons, most of which have to do with the fallout of the pandemic. The spring of 2020 was sheer chaos as we were all trying to figure out how to teach virtually. The 2020 – 2021 academic year saw a multitude of rules restricting how we could interact with each other when we were in person (which, for our school, was the great majority of the year) and a couple of retreats into virtual schooling. I had students in front of me and students on my computer screen all year long (at least when we could have people in the same room!) and I know I was not alone in learning how to deal with that. I had all my students seated in rows and columns for the first time in 15 years and I had to try to relearn how to look out at a class like that. We could not sit in groups and share ideas with our neighbors at our elbows. I could not roam around the room and look over people’s shoulders and quietly share ideas and questions. None of this is news to anyone who is reading this. What I am trying to figure out is what tools/habits I’ve developed in the past fifteen months are worth carrying forward into the 2021 – 2022 academic year and beyond. There is a cliche about not wasting a crisis and I had some pretty meaningful conversations with my students about the ‘new normal’ this year. I laid out some practices that I had adopted, practices that were not part of my repertoire before COVID days. I asked them what was worth keeping and what they would be happy to never deal with again. The three features of life this year that got the biggest endorsements were (1) Scanning and submitting written work so that they could access their work and my comments at a later time. (2) My inclusion of DeltaMath into our life. (3) My use of BitPaper for classroom notes.

I want to think out loud about each of these three features.

1 – Obviously, any paper submitted and returned with notes/corrections/remarks is retrievable, even in COVID times. However, my students were really honest about their lack of organizational skills. Most papers that ever got returned got shoved into backpacks, ended up at the bottom of a locker, on the floor of their car or their bedroom, and were not accessible when it came time to study or reflect. I did not enjoy writing on their work through the google classroom and within the Kami environment. But if even a small portion of my students actually went back to the Google classroom page later to reflect, then it might (might!) be worth that time and effort.

2 – I was way too late to the DeltaMath game. I think Zach’s work there is tremendous and I got so much positive feedback from kids about the guided practice and videos available to them there (I paid for a plus membership so my students have limitless (I think it is essentially limitless) access to carefully presented videos to help them work out mechanical issues and to be reminded of why math life was unfolding the way that it was.

3 – I don’t know how many people know this tool. Here is an example of one of my BitPaper note pages https://bitpaper.io/go/Bell%206%20Calc%20Hon%20Week%20of%20May%2010/HJpuKAieh

I set up a new page for each section each week so that the pages would not get TOO cluttered. I did not write on a whiteboard at the front of the room at all this year. I did all of my writing on BitPaper and students had access to these pages at any time. There are some tweaks I wish they would make. I wish there was a scroll bar to move up and down the page. I wish multiple kids could view at the same time without interrupting each other. The second wish might be a lack of understanding on my part. But that is not what I want to write about. I want to talk about what I see as a huge advantage. My students can listen in on my conversation and what their classmates are saying. They can jot down quick notes or reminders to themselves, but they do not have to feel any pressure at all about transcribing while listening. They can look at class notes later and listen and think more efficiently in real time. I had a discussion about this tool and about the fact that I intend to use it again next year (or a different tool that might be better if someone can steer me to one!) and the response I got was that note taking is a vital skill and they need to work on this. I tried not to react negatively but inside I was sure feeling some serious skepticism about this claim. It feels obvious to me that listening and thinking and talking are more important than being a stenographer. If I am wrong here, if I am missing something important, I hope to hear it either in the comments or over on twitter where I am @mrdardy

There were SO many new tricks/tools that I tried this year but these three were the ones that resonated with my students. I would love to hear some reaction to these ideas and also hear about successful new tools/ways of thinking that infected your classroom during the pandemic.

Looks Like We Made It

Yesterday was the last day of classes for the 2019 – 2020 academic year at my school. I have an awful lot to unpack in the next couple of weeks about how the spring term unfolded. What I want to share tonight is how my last week went.

I teach five classes, three different preps. I teach one section of AP Calculus BC, two sections of Calculus Honors (our non-AP course in Differential Calculus), and two sections of Precalculus Honors. For my Calc Honors and Precalc Honors sections I set up a calendar for students to sign up for twenty minute ‘exit interviews’ with me. Last week on our google classroom page I posted a set of ten problems – a sort of mini final exam. I told my students that when they met with me I would randomly generate two numbers and they would explain those problems to me. It went pretty well. It was great having one on one time with each student and they mostly did a nice job of explaining problems that ranged throughout our year together. But what was fun was our brief conversations after the math. I asked each student to imagine that time travel was possible. I then said ‘What if I had taped this conversation over the last ten minutes and went back to August you to let her see what May you is up to?’ The reactions were pretty great. Almost every student said some for of ‘I’d be pretty amazed by what I can do’ or ‘I wouldn’t believe that I could make sense of those problems’ That, of course, was my point. I wanted each of them to have a brief, reflective moment where they thought about all that they had accomplished in the past nine months.

It has been a hard couple of months but I ended my day on Thursday all zoomed out (46 meetings in four days plus a couple of AP Calc group meetings) but I felt really good about this decision on how to end the year and about my silly time travel prompt.

Time to rest for a few days now…

Observations

Yesterday our school announced that we are to be physically closed until Monday, April 27. At that time we will re-evaluate our situation. Graduation is scheduled for May 24. This is hard news to digest. I understand that many many teachers and parents and students are digesting similar news right now.

At breakfast this morning my ten year old daughter said ‘I don’t like virtual school’. She then made a couple of remarks that I should remember exactly, but I don’t. I’ll paraphrase her – ‘I think that there should be some separation in our life. Home is for relaxing, snuggling with my kitties, and fun. School is where I focus and work on learning. It’s hard to do that in my room.’ What she did not touch on, but she definitely mentioned last week when all of this started for us is that school is where her friends are. FaceTime chats are fun, text chains can be as well. None of it replaces being around people.

I have made a commitment at this point (only four class days in so far) to hold zoom meetings for all of my 50 minute classes. For our 90 minute meetings I am setting up 10 minute one on one sessions. I don’t know how sustainable this all is, but the reassurance of seeing and hearing each other feels really valuable. Early survey results indicate my students feel the same way.

Bragging About My Students

Holiday break began yesterday and I find myself with time to breathe and (hopefully) get some real writing done. Before thinking about work for January, I want to take some time to pause and reflect on some of the great stuff my kids were doing before the break.

I found this problem on twitter and shared it with colleagues and classes last week:

My memory is that this image was accompanied by a simple ‘What do you notice?’

It took me a minute or two to notice what was happening. I showed it to a colleague who started chuckling instantly. He has a faster mind than mine!

So I showed it to my classes, they all eventually noticed that the digits 1 through 9 were all used in this equation. My challenge to them was to write an equation using the digits 0 through 9, once each, that was also true. I urged them to not simply add a zero to one side of that equation above.

The kids dove into this challenge and came up with some great solutions. I have a photo I took on my iPad with some of their solutions superimposed on the image of the original problem.

The top right equation is missing the 9 on the right side of the equal sign

Fun, right? Even better is the fact that some kids were still working a couple of hours later coming up with ever creative solutions. My favorites were both cooked up by a student who had a sub in his Health class (me!) and he was tinkering with this problem at that time.

This one won my heart, I must admit.

I hope to do some more writing in the next two weeks. Some will be public, some will be piles of problem sets for my kiddos.

Brief Post – First Days

Busy busy start to the year. I want to take a moment to reflect on and remember a couple of important highlights.

Opening Day

We meet all classes for 30 minutes on day one and we have an hour long convocation ceremony. Our Student Body President is always one of the speakers. This year’s President was in my Precalculus Honors course last year. She delivered a touching speech about productive struggle in my course last year – a course she ended up excelling in, by the way. I have heard a number of speeches by adults advising the importance and lasting power of productive struggle. I imagine that this speech by one of their colleagues probably meant more to our students than hearing some grown up tell them about the glories of allowing yourself to struggle through something. The fact that she highlighted the very things I hope my students take away from my class made it pretty special. The fact that the whole upper school community (and my immediate supervisors!) heard it as well made for a pretty special opening day.

Regular Old Day One

My day started with my AP Calc BC team. I had assigned a HW problem I had never done before. They were asked to graph x + |x| = y + |y|

The table group that had this problem struggled a bit and we talked it through as a group. We then called on Desmos to graph it and the result was not what we thought it should be. I did what I do, I tweeted out the problem and within fifteen minutes one of my former advisees tweeted out a fix so that Desmos would agree with us. It is delightful to have that connection with a student who my current students still remember. It was also fun to think that my questions are still interesting enough to warrant his attention.

There will be some rough days this year, there always are. I want to remember days like this so it is easier to get through the tough ones!

Thinking About Speed and Time

On first glance, the title of this post has me thinking about my Calculus classes, but that is not the speed and time angle that is on my mind this morning. Yesterday, I finished listening to the newest episode of Malcolm Gladwell’s Revisionist History podcast. The episode (found here) is called Puzzle Rush which is the name of a variant of chess. In the episode Gladwell raises some interesting questions regarding chess, the LSAT, and various places in our society where it seems that speed is valued more than deep thought. He keeps referring to the hare and the tortoise and wonders when the hares got to make the rules. This pod has me thinking about my assessment practice. As I often do, I am going to use this space to think out loud and I am going to hope for the usual outpouring of wisdom here and on twitter to help me work through my questions/concerns.

Earlier this year, some colleagues were having a grumpy conversation about the kids these days. You know, the usual grumpy late winter talk about what is wrong with kids. A totally natural conversation that happens at some point every year. Not a criticism here. However, I did push back a bit and I said that while my current Calc BC kids would be dismayed by my Calc BC tests from 20 years ago, my kids from 20 years ago would also be dismayed by my tests from today. I am pretty convinced that my students today are being asked for deeper analysis of why the math they have learned works the way it does and they are asked to make more predictions and asked to tie together information more deeply. I am also pretty convinced that they are slower in their calculations and in their algebraic manipulations. If my students from today tried to complete in 50 minutes a test I wrote more than a decade ago, many would flounder. If my students from ten years ago tried to complete a test I wrote this year, many would be flustered by the open nature of some of the questions. In general, I think that the thinking I am asking for now is more important. If I still thought that the old ways were more important, I would not have evolved in my assessment practice in the direction I have moved. Where Gladwell has me questioning myself is that there is still a distinct flavor of speed that comes into play. I have a number of students who are still furiously writing when I give them a three minute warning. They are still furiously writing when I give them a one minute warning. Heck, they are still writing as students are passing from class to class in the hallways and I have to bark at them a bit to give up their work. I am somewhat convinced that this might be true no matter how much I shorten the tests. I also admit, not proudly, that I am a little uncomfortable with the idea of a 50 minute class test only taking 20 minutes for some of my best students. I do not believe that speed is the best judge of talent, I know better. But I also suspect that speed is an ingredient in success in many endeavors. What I am wrestling with in the wake of Gladwell’s pod is how do I strike a balance here. I keep flashing back to an essay I read years ago by Dan Kennedy in which he advises ‘Value what you assess and assess what you value.’ I think that there is a very real part of me that values some level of automaticity. Maybe I am being shallow here, but it feels like my best students, the ones who have really mastered ideas, can do so quickly. Maybe I am just fooled into thinking that they are my best because they move quickly? I can keep rambling with this internal monologue, but I won’t bore you this way. I will just jump to some questions that I have for you, dear reader, and I hope to get a nice conversation going in the comments here or over on the twitters where I am still @mrdardy

  1. How do you estimate the time needed for your students to complete a task in class? I have 50 minute classes (mostly) for testing. I generally work on the idea that I should be able to carefully write out my solutions in about 15 minutes. No real science behind this, just accumulated experience.
  2. When writing a test where I am pretty sure that there is one especially challenging (I usually call them interesting!) question, I try to place that one near the front half of the test. Students can, of course, skip around but most just plow through. I want the problem requiring the most thought to be placed where there is still some time for that thought to occur.
  3. When students finish their test, they are dismissed. Is this smart? How do you approach this?
  4. Our schedule, like many of yours I would guess, does not really encourage flexibility with students who might want that simple two to three extra minutes to wrap up work. I have students coming in for their class and I want to respect their time. My students are on their way to their next class and I do not want to interfere with that time. I am uncomfortable, for a number of reasons, with the idea of having them just come back to wrap up later. Any comments/ideas/hacks that have worked within these pretty common scheduling restrictions?

As always, thanks in advance for any wisdom. I am looking forward to a good conversation that will benefit me and my students.

Balancing Group vs Individual Work

For over ten years now, my classroom has been setup for group work and talk. Currently, I have desks in groups of three and I reshuffle the groups after five class meetings using flippity. One of the courses I teach is called Honors Calculus. It is a differential calculus course that is an option instead of AP Calculus AB. What is typically done be the first week of December in the AB course takes us into May. This allows much more time to review algebra and trig ideas and to really dig into the mechanics and principles of Calculus. I don’t skimp on the level of analysis I ask for in this class, we just have more time to settle in. This year, after a conversation in the first trimester, I settled in to a routine where we have group quizzes – I write five versions of each quiz – but we have individual tests. My hope was that this would decrease the level of stress in the classroom, that it would increase the level of communication between the students, and that hearing multiple voices would increase the likelihood of ideas and techniques sticking with my students. What I have witnessed is that this process has decreased the level of stress overall because a handful of students just don’t worry much knowing that they are paired with confident kids who can carry them to the finish line, the level of conversation HAS increased, but only for a subset of the students who end up in the role of explainer, and ideas are NOT sticking. Mistakes made in November are still being made. Skills practiced (or at least skills that have been available for practice) are not embedded. On our most recent individual test about 15% of my kids did not recognize the need to use the product rule when taking the derivative of a product. I have asked a variation of the exact same question for the last three tests and there is no noticeable improvement in answering that question.

There is another feature of our class that is at play here. In the 2017 – 2018 academic year our department adopted a test corrections policy that I wrote about previously. For the 2018 – 2019 academic year the department voted down this policy. I had spent a considerable amount of time and energy promoting this policy and talking about its importance in the learning process. In the wake of this decision I reached an uneasy compromise with the two courses where I am the only instructor. They can review a test when it is returned and they can reassess on up to three questions from that test with the possibility of earning up to half of the credit they missed. There was a lot of debating in my mind and with my students before we arrived at this imperfect solution. This was in place before the conversation with Calc Honors about group quizzes. Looking back, I feel that the combination of group quizzes AND opportunities to reassess provides too much of a sense of safety net and many of my students are pretty clearly not preparing themselves too carefully or they are simply not practicing much. With the level of practice opportunities provided/the number of times to talk together in class/the class conversations led by me with examples and old assessments offered as practice/etc. I simply should not be seeing the test performances I am seeing. I am clearly complicit in all of this due to the decisions I made about assessment and the decision I have made not to collect or check HW practice. In my last post I thought out loud about the idea of frequent, low stakes, skills-based check in assessments. Had a great twitter chat last night with the #eduread crew (prompted in large part by this article ) and I went to sleep convinced that I need to incorporate some of these ideas into this course next year. I also need to remove the added layer of reassessment, it has not worked in conjunction with the group quizzes. I think I probably still need group quizzes separate from the check-in layer of ways for me to see progress AND as ways for kids to feel that they can buffer their grade with legitimate skill progress. I hope that the combination sends a couple of important messages about what I value. I really (REALLY) like the conversations that do happen in the group quizzes. I am more than willing to write multiple versions of quizzes so that conversations can happen out loud without worrying about giving away information. Our discipline, I think, allows this more easily than some others might. I do not want to collect HW daily for all sorts of reasons, but I think that frequent low stakes check ins send a message about the importance of mastery of topics. I think that I need to adjust my problem sets so that they feature more reminders of topics. My kids know how to take derivatives with the product rule. They probably need to be periodically reminded of it in a more tangible way. I also wonder about balance in point values between these three ways of assessing and reporting on my students’ progress. I do not want to retreat into a mode where I am scaring (or bribing) my students, but I do think I need to be more clear and explicit about what I value and balance it accordingly when/where I can.

As always, any words of wisdom here or over on the twitters (where I am @mrdardy) are much appreciated.

Thinking Out Loud

Been too long since I wrote, all sorts of reasons but none of them meaningful enough really.

I often use this space to air some thoughts and questions and I always value the conversations that ensue either here or over on twitter (where I can be found @mrdardy)

So, here is what I am pondering now and would love to hear some pushback or validation or further questions to help me organize my thoughts. For years – all 32 of them in the classroom – I have told my students that I do not believe in pop quizzes. I said that I do not want quizzes to be seen as punitive, I don’t want them waiting for me to play ‘gotcha’ with them. Similarly, I don’t do surprise HW checks or anything like that. However, I am thinking that I might have been wrong about this. I see (so often!) kids frantically studying (cramming) knowledge into their brains for a short term amount of time with the intent of performing some data dump on their quiz. I have even had students argue that they do not want me to answer any lingering questions from their classmates because they don’t want to forget before the quiz. As if 8 extra minutes will somehow erase meaningful understanding. However, the more I think back on these, the more I realize that the message being sent to me in these conversations is that there is not meaningful long-term knowledge that the students think is their job. Just be able to reply and re-present skills/techniques. I think I do a pretty decent job of asking interesting questions that encourage/allow/demand some real thinking and some really knowledge to be displayed. But if every assessment is announced and planned for and worried about, then I suspect that I am not really getting a meaningful picture of any developing understanding that my students are working on. I wonder if periodic low stakes check ins would be a better use of my time AND a more true picture of what the students are understanding. These check ins would take less time allowing us to have more time to talk/debate/discuss (heck, just BREATHE) in our time together. These would occur more frequently giving me more granular data, more of a sense of continuity in charting their understanding. They would not be a source of stress at home and they might (might!?!) send a different, more meaningful message about what my goals of assessment are. A downside is that these feel like they would be more directed at quick skills check ins rather than meaningful, complex and connected questions. those questions take more time, they might not be at home on a quick exit ticket (or entrance ticket?) type of check in. If I do enough of them – or if I build a system with some drops/mulligans – then any particular ‘bad day’ would not have much of an impact. If I am thoughtful about these and I enact Henri Picciotto’s ideas about lagging HW and think of these as lagging assessments, then the notion of a busy night for school or family activities, would not be a meaningful argument about why a particular quiz might be below par. If I lean in on this idea, I think I would move away from my current practice of quiz / quiz / test rhythm in many of my classes. I would probably feel less stressed about time taken for assessments and would feel that there was reasonable data about student performance and understanding. I have adopted a system of problem sets in two of the three courses I teach, open problems that are sometimes thorny but the students have seven school days to complete them and they are encouraged to collaborate on these assignments. This feature also helps ease the concern about grades to a certain degree.

So, I guess what I am asking dear reader are these questions –

Are unannounced assessments inherently unfair?

Are check ins on developing understanding reasonable data to register and count (in some way) as part of the report on progress that is expected at my school?

Is the habit of cramming an inherent part of the problem that we math teachers see all the time – Fragile knowledge or simple lack of ability to recall and reorganize information that has (allegedly) been learned in previous courses?

Thanks in advance for any wisdom shared here or over on twitter

A Residue of Professional Development

So, the session I wrote about a few days ago (you can find that post here ) continues to pay dividends. Yesterday my Precalc Honors kiddos had a test. Today we were to begin discussing vectors. I had what felt like a pretty clever idea this morning. I started off by posting this image (stolen from the opening evening problem that Amy and Allyson shared with us )

I simply asked ‘How many squares can be formed?’

I got a quick question back asking if the dots were equidistant. I confirmed and then my students began to quietly count. I encouraged them – as I always do – to chat with each other and I was hearing things about medium sized squares, big squares, etc. I suggested that some more formal classification might be helpful. A couple of kids quickly concluded that there are 30 squares to be formed. This is a correct answer under certain restrictions. unfortunately, these restrictions were not placed on the question. A student named Max said 40 out loud, then said 50. This shook up the crowd a bit and people began to dig in. However, they were hesitant to debate Max because he has a reputation (well deserved) for being pretty on point with questions like this one. SPOILER ALERT: I AM ABOUT TO UNVEIL OUR SOLUTION. IF YOU WOULD LIKE TO AVOID THAT AND THINK ABOUT IT FOR AWHILE FIRST, COME BACK LATER.

Still with me? Good, happy to have you. I went to the board and drew a square of side length sqrt(2) and got two great reactions right away. One person called this a diamond but acknowledged it is also a square. Another said we should redefine squares to avoid this. I then stepped out of the way to encourage discussion about sizes of diamonds that could be formed. We had a list on one side of the diagram listing number and size of ‘squares’ and developed a list on the other side of the number of, and size of, the different diamonds. We had some great debates about the parameters here. We decided that the only diamonds had size lengths of sqrt2, sqrt5, sqrt8, and sqrt10. We were unsatisfied with the seeming lack of a clear pattern here. You will see in the picture below how I tried to impose a little bit of order on the counting by making sure that I identified groups of diamonds or squares in numbered sets that were all perfect square integers in their count. What you will also see in the picture (coming soon, I promise!) is that I pivoted the conversation soon to vectors. My Precalc Honors kiddos took a test yesterday and we are prepared to start a new chapter on vectors. I did not particularly advertise that this was the next topic, but it felt like I could pivot in that direction. Many of the kids in this class took Geometry at our upper school with a text I wrote. In that text, I intentionally introduce some vector language early in the year. When I got to school today, I did not intend to pivot from this diagram straight into talking about vectors, but when we were discussing diamonds of length sqrt5 I realized that it was meaningful to distinguish between a horizontal change of 2 with a vertical change of 1 versus a horizontal change of 1 and a vertical change of 2. Time for the photo now and then a little more explanation.

The end result after our launch into vector conversations. Note that diamond count is written as 4 + 4 and 1 + 1 for different sizes. Trying to focus on perfect square counts there!

So, in the photo above, a bit of glare there unfortunately, you see a green side of delta x = 1 and delta y = 2. I drew an arrowhead and one student muttered ‘vectors!’ It felt like such a natural trigger and frame to discuss vector notation. Almost instantly kids were discussing magnitude, direction, remembering notation, etc. Man, it was a great way to start the day!

I ended up sharing this problem with a couple of other classes during the day and each time I confessed that my partner and I only found 45 squares and were VERY confident of our answer. Each class figured out where we had gone wrong and they seemed pretty proud that we worked through this all together.

Another opportunity here to thanks Amy and Allyson for the great PD session and I know that I will be pulling some other tricks out of the bag of tools that they provided for us last week.

Meaningful Professional Development

Back in November we were having conversations at our school about improving our ability to place new students in our curriculum. Every year we have a wave of brand new students who have to move down from our original placement suggestions and it is always a frustrating thing for them and for us. So, I did what I do and I reached out to a number of department chairs at schools like ours seeking advice. One of the people I reached out to was Amy Hand. She is the math chair at Packer Collegiate Institute in Brooklyn, NY. In addition to sharing some wisdom, she also mentioned a workshop she was putting together. Here is the flyer she sent me –

I was immediately intrigued and I went to my admin to pitch the idea. We decided that we could afford to send a handful of folks together there and we ended up inviting our two Geometry teachers and one of our middle school teachers to go with me. I have been on the inquiry bandwagon for awhile but I knew that I could learn some new wrinkles to add to my game. I was excited to bring along three colleagues to listen to someone other than me pitch this idea. I also knew that the power of being in a room together working side by side with colleagues is always a powerful thing. Well, we returned Friday afternoon and I have had a couple of days to let some of the ideas sink in – as well as a couple of days to get caught back up with my life here. I am happy to spend a little time here telling you about what a wonderful experience this was. I feel that there is some positive energy that can help move our department forward in examining how to open up our classroom culture to encourage more open inquiry from and for our students.

Amy and Allyson Rohrbach, a colleague of hers from Packer, put together a really meaningful and packed two days for us. We started with a short introductory session on Wednesday night. This seemed like an unusual idea, but it was a great way to start. We had what seemed like a completely innocent problem on our tables. It was a problem from Brilliant that involved counting squares. I wish I had the image of this problem, perhaps I can find it soon to share. What seemed like a completely innocent problem instead became a lovely conversation about counting procedures with different folks going to poster paper at the front of the room to share their strategies. We got to know each other over snacks and beverages and discussing math ideas, Amy and Allyson framed our work efficiently that night and I think that we all left the room that evening energized for our work the next day. Thursday was the heavy lifting day but even that was paced really well and Any and Allyson kept us shifting gears so we did not feel like we were sitting with one idea or one problem for too long. There was plenty of space to explore and I don’t think that any of us felt rushed. One of the problems we worked on is one that Amy and Sam Shah worked on together at Packer and Sam blogged about that problem here I know that the next time I am teaching Precalculus I will be framing our discussion through this problem. I feel certain that I read Sam’s post when it came out, but working side by side with folks in this environment brought the problem and the pedagogy behind it to life in SUCH a meaningful way.

Again, we had GREAT conversations discussing/debating/explaining ourselves. I certainly have fun listening to my students debate like this but there is a different level of fun when I can get lost in the math myself to this degree. It is also energizing to hear from and share with people that I have never met before. There is such a sense of open curiosity in a carefully designed environment like the one that Amy and Allyson helped create.

I walked away from this event convinced that I will have an ongoing exchange of ideas with Amy and Allyson and I am already discussing a school visit to bring some of my colleagues who did not make it to this event. You can follow Amy and Allyson over on twitter where they are @MathSenseLLC. you can also check out their next workshop which is described here They will be on the west coast for this trip. If this is more in your neighborhood and you want to be recharged in your commitment to inquiry driven education or if you want to be nudged in this direction, I cannot recommend this highly enough.