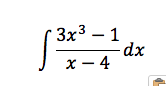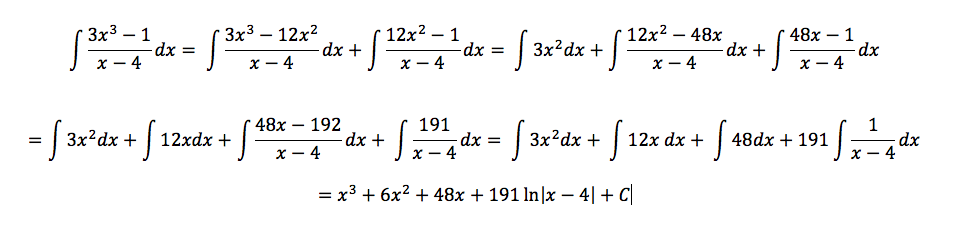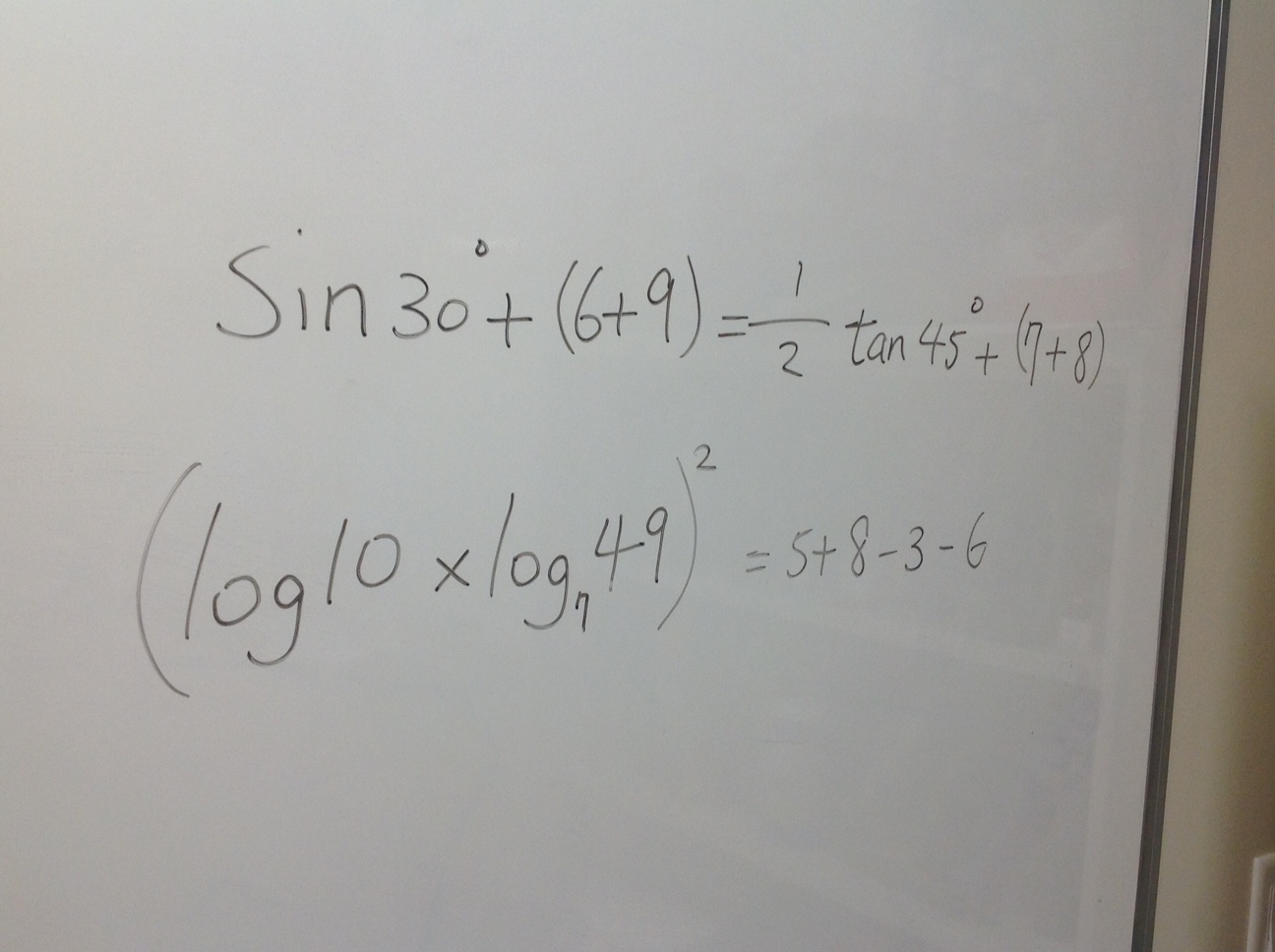I am in my twelfth year at my current school and my family has lived on campus the whole time. We spent our first six years here living in a boys’ dormitory with over 80 teenage boys from all around the world. I enjoyed my time in the dorm but after six years we graduated to a campus home two blocks away from my classroom building. A few weeks ago my son decided, around 11 PM one night, that he wanted his head shaved the next day. He reached out to his friend text group to find out who was free during the last period of the day to help him with something. I, of course, did not find out about this until the next day when he casually mentioned that a friend would use my set of clippers to cut his hair during his free period at the end of the day. That friend happens to be one of my students, so I heard about this form him as well. During the course of the day word spread and a number of students who are free that period planned on coming over to watch and some livestreamed the event on Instagram. My son told me that as he was walking over to our house for this he was talking with some friends on the way. One of them made a remark to the effect of ‘this is why our school is so great.’ Now, of course, I could grumble and say that our school is great because of what goes on in the classroom, the stage, the athletic fields, the dorms, etc. I believe that there are a number of reasons why our school is a special place, but I realize that adventures like this one add a real spice to the day. The kind of communal, shared experiences, especially silly ones like this, help make being in a community more memorable and I have to realize that watching a friend shave another friends hair on a sunny early winter afternoon might be a more memorable experience than learning the Law of Cosines or something along those lines.
When my wife and I made the decision to move to a boarding school community I think that something along these lines was in my mind. The idea that my children get to be immersed in a community, they get to call their campus home as well as it being their school seems to be pretty powerful. I wonder whether they will become as sentimental about it as I am. Time will tell.
PS – It ended up being a pretty good haircut.